Fractals déterministes (scalants) / Autosimilitude
1. La variété infinie des échelles d'examen
Selon le point de vue propre à la géométrie fractale – qui rejoint là, d'ailleurs, celui de la géométrie euclidienne –, les objets de la nature, observés à grande distance, peuvent apparaître globalement comme des formes simples, régulières, descriptibles au moyen des modèles formels de la traditionnelle géométrie euclidienne : des points, des lignes, des cercles, des triangles, des parallélépipèdes, des cubes, des sphères, des cônes, des cylindres, des polyèdres, et toute combinaison de ces formes élémentaires primitives. D’ailleurs, le peintre Paul Cézanne (1839-1906) disait qu’en peinture il convient de traiter les formes de la nature par ces figures géométriques élémentaires, mises en perspective.
Pourtant, observées de plus en plus près, éventuellement au moyen d'une loupe, ces formes naturelles apparaissent beaucoup plus compliquées, plus morcelées et fragmentées, beaucoup moins continues que supposées et, en un mot, fort peu « euclidiennes ». Elles présentent des contours brisés, discontinus, rugueux, fractionnés, et des structures ramifiées, enchevêtrées, remplies de micro-détails : ce sont des objets fractals (ou, plus brièvement : des « fractals »). Si le niveau de résolution, toujours plus exigeant, continue de s'affiner par l'intermédiaire de la loupe et du microscope, le moindre détail apparaît alors comme étant composé d’une myriade de détails plus fins, toujours plus riches de microformes dispersées, elles-mêmes saturées à l’infini – en théorie tout au moins, car la nature ne peut être sondée « à l’infini » ! – de nouvelles microformes emboîtées, hyper-détaillées, aux aspects imprévisibles. Telles des poupées gigognes, les microstructures de la nature s’imbriquent l’une dans l’autre, selon une hiérarchie multiscalaire (c’est-à-dire à une multiplicité d’échelles emboîtées) pourvoyeuse à l’infini de structures morphologiques nouvelles, irrégulières et enchevêtrées.
Ce sont les différents niveaux d’échelles d'examen de l'objet (théoriquement en nombre infini) naturel ou géométrique, qui définissent les degrés variables de discontinuité et de dissymétrie. D'ailleurs, en toute logique, si un fractal déterministe (scalant) régi par une loi d'homothétie interne, comme la courbe de Von Koch et celle de Peano par exemple (objet idéaux, purement mathématiques), possède une unique dimension, en revanche un objet réel est représenté en fonction de différentes échelles de description ou d'observation qui déterminent alternativement autant de dimensions différentes, fractales (non entières) ou topologiques (entières, euclidiennes). Le thème, évoqué en physique quantique, de l'interrelation opératoire de l'observateur avec l'objet observé, se présente dans le champ de la géométrie fractale, comme le principe même du calcul de la dimension fractale. Il existe, en effet, une forte analogie entre la géométrie fractale et la mécanique quantique : dans les deux cas, la présence de l’observateur ou du descripteur modifie le résultat de l’expérience en cours.
Cependant, pour conserver la justesse du raisonnement, l’analogie s’arrête là, car en mécanique quantique, la présence même de l’observateur et de ses instruments de mesure, comme éléments de la réalité physique, constitue un facteur de perturbation et donc de variation de la mesure. Tandis que dans le cas des objets fractals, le résultat se modifie seulement en fonction du point de vue défini géométriquement par programmation, c’est-à-dire selon le niveau d’échelle mésoscopique auquel on décide de s’arrêter : intermédiaire (sens du préfixe grec « méso ») entre un niveau « macro » supérieur, et un niveau « micro » inférieur. Les deux situations sont, pour cette raison, très différentes.
2. Fractals déterministes (ou « scalants »)
Il existe une multitude d’objets fractals (ou de « fractales », au sens général des figures fractales) plus ou moins complexes et irréguliers. Les plus simples d'entre eux – dits « auto-identiques » ou « scalants » –, se répliquent exactement à l’identique à toutes les échelles de grandeur, et possèdent pour ce motif la propriété géométrique dénommée « autosimilitude » (par homothétie interne), qu'il ne faut pas confondre avec l'autosimilarité (statistique, stochastique) des fractals aléatoires ou semi-aléatoires. Tout détail (local) réplique exactement à l’identique, le tout (global) à partir duquel il est construit, seule l’échelle de grandeur varie : c’est la loi d’homothétie interne, formulée par Benoît Mandelbrot.
Les objets fractals scalants sont obtenus par des opérations géométriques répétitives, invariables, strictement déterministes, sans aucun mécanisme ou événement aléatoire qui puisse introduire de la différence morphologique – sauf la différence scalaire –, telle la courbe en « flocon de neige » de Helge Von Koch (mathématicien suédois, 1870-1924), la courbe fractale dite « courbe remplissante » construite par le mathématicien italien Giuseppe Peano (1858-1932), ou encore, parmi les fractals géométriques les plus connus, le tapis fractal du mathématicien polonais Waclaw Sierpinski (1882-1969), ainsi que, parmi une infinité d'objets fractals scalants possibles, l'ensemble triadique de Cantor (Georg Cantor, mathématicien allemand d’origine russe, 1845-1918), communément appelé « poussière de Cantor », car il est constitué d'une myriade de points en fragmentation (virtuellement) continue. Georg Cantor a créé la théorie des ensembles, en collaboration avec le mathématicien allemand Richard Dedekind (1831-1916).
Une modélisation artistique approchée des fractals scalants (auto-identiques), à l’époque de la Renaissance italienne (au Quattrocento), fut donnée dans un traité de peinture intitulé Le Livre de l’art ou Traité de la Peinture (1437), par le peintre florentin Cennino Cennini (v. 1370 – v. 1440) qui décrivit, pour la formation des jeunes peintres, une méthode de création de type « fractaliste ». Il leur conseillait de peindre les montagnes avec le maximum de vérité morphologique, en partant du regard posé sur une simple pierre pleine de brisures et d’irrégularités, tout en faisant varier les projections de lumière sur cette pierre : « Si tu veux faire des montagnes d’un bon style et qui paraissent naturelles, prends de grandes pierres pleines de brisures et non polies, copie-les d’après nature en faisant venir la lumière et l’ombre dans la direction qui te convient. » Cennino Cennini, Le Livre de l’art (Il Libro dell’arte, 1437), 3è section, § 88, éd. F. de Nobele, Paris, 1982, p. 67).
L’artiste italien avait compris avec perspicacité, que la partie d’un ensemble (la pierre) porte en elle – en raison de la propriété d’auto-identité fractale (ou autosimilitude) entre le tout et les parties – le principe de construction intégrale du tout (la montagne). L’observation, aidée de la projection adéquatement orientée de faisceaux lumineux, met alors en évidence l’analogie morphologique existant entre le détail et le tout. La montagne, vue en sa totalité, est trop complexe pour être décrite avec précision ; c’est pourquoi le principe de réplication homothétique du détail par autosimilitude formelle, potentiellement « à l’infini », propose un modèle géométriquement pertinent de la forme globale de l’objet. La méthode de représentation picturale des montagnes (et en général des objets naturels irréguliers), n’est donc, pour l’artiste de la Renaissance italienne, nullement différente de la construction déterministe des innombrables objets fractals scalants, obtenus par réplication homothétique indéfinie (« homothétie interne » de Mandelbrot), telle la courbe en « flocon de neige » de Von Koch.
En résumé, les fractals « scalants » (ou auto-identiques), obtenus par un procédé opératoire strictement déterministe, répètent à l’identique le même motif de base, à toute échelle de grandeur imaginable. Par conséquent, toute partie et le tout dont elle « provient », sont morphologiquement identiques, mais à un facteur de réduction scalaire près, dénommé en géométrie : coefficient de réduction homothétique. Le « flocon de neige » fractal de Von Koch et la « courbe remplissante » de Peano en sont des illustrations typiques.
3. Dimension fractale de la courbe en « flocon de neige » de Von Koch
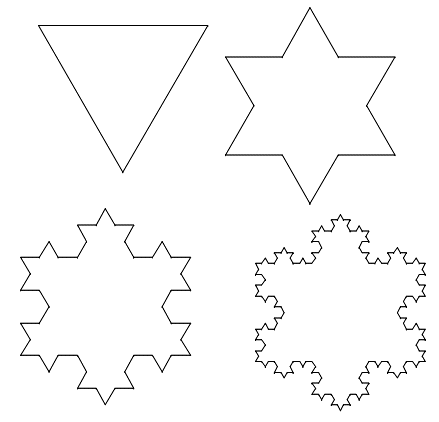 La courbe en « flocon de neige » de Von Koch (1904) – sans doute la plus populaire des fractales déterministes – est obtenue « à l’infini » par un algorithme itératif, comme toute les fractales. Son périmètre théorique est infini, mais sa longueur réelle demeure finie. On l’obtient – de manière approchée – en opérant sur chaque côté d’un triangle équilatéral, une suppression de son tiers central, pour construire à la place 4 segments de valeur 1/3. Chacun des anciens côtés de valeur 1 devient donc égal à 4 fois 1/3 soit 4/3, et le triangle équilatéral de base a pour longueur, après la première transformation, 3 fois 4/3, soit 12/3 = 4. À la première étape, la figure ainsi transformée comprend donc 12 côtés de valeur 1/3. En réitérant indéfiniment la double opération de suppression du tiers central, et de remplacement de chaque côté par 4 côtés égaux à 4 fois 1/3, on obtient un contour hyperdentelé qui paraît tendre vers une courbe continue, mais sans jamais s’y réduire. Comme toutes les figures fractales, la courbe de Von Koch n’est pas « rectifiable », c'est-à-dire qu'il est mathématiquement impossible de calculer sa dérivée en un point quelconque de son périmètre, infiniment discontinu à toute échelle de calcul.
La courbe en « flocon de neige » de Von Koch (1904) – sans doute la plus populaire des fractales déterministes – est obtenue « à l’infini » par un algorithme itératif, comme toute les fractales. Son périmètre théorique est infini, mais sa longueur réelle demeure finie. On l’obtient – de manière approchée – en opérant sur chaque côté d’un triangle équilatéral, une suppression de son tiers central, pour construire à la place 4 segments de valeur 1/3. Chacun des anciens côtés de valeur 1 devient donc égal à 4 fois 1/3 soit 4/3, et le triangle équilatéral de base a pour longueur, après la première transformation, 3 fois 4/3, soit 12/3 = 4. À la première étape, la figure ainsi transformée comprend donc 12 côtés de valeur 1/3. En réitérant indéfiniment la double opération de suppression du tiers central, et de remplacement de chaque côté par 4 côtés égaux à 4 fois 1/3, on obtient un contour hyperdentelé qui paraît tendre vers une courbe continue, mais sans jamais s’y réduire. Comme toutes les figures fractales, la courbe de Von Koch n’est pas « rectifiable », c'est-à-dire qu'il est mathématiquement impossible de calculer sa dérivée en un point quelconque de son périmètre, infiniment discontinu à toute échelle de calcul.
[↑ Figure 1 ci-dessus : Courbe fractale de Von Koch, étapes 1 à 4 de sa construction.]
 Cette courbe irrégulière en forme de flocon de neige dentelé possède ad infinitum un périmètre de longueur infinie, bien que sa surface fermée demeure finie. On démontre que la dimension fractale de la courbe de Von Koch est égale à D = (log 4) / (log 3) = 1,261..., donc supérieure à la dimension topologique d’une courbe idéalement continue de la géométrie euclidienne (D = 1), mais inférieure à la dimension topologique d’une surface plane euclidienne (D = 2). Il s'agit d'un être mathématique intermédiaire, plus qu'une ligne euclidienne parfaitement lisse et continue en tout point, mais beaucoup moins qu'une surface enveloppante fermée, aux bords idéalement continus. [↑ Figure 2 ci-dessus : Courbe fractale de Von Koch, étape n de sa construction, n tend vers l'infini.]
Cette courbe irrégulière en forme de flocon de neige dentelé possède ad infinitum un périmètre de longueur infinie, bien que sa surface fermée demeure finie. On démontre que la dimension fractale de la courbe de Von Koch est égale à D = (log 4) / (log 3) = 1,261..., donc supérieure à la dimension topologique d’une courbe idéalement continue de la géométrie euclidienne (D = 1), mais inférieure à la dimension topologique d’une surface plane euclidienne (D = 2). Il s'agit d'un être mathématique intermédiaire, plus qu'une ligne euclidienne parfaitement lisse et continue en tout point, mais beaucoup moins qu'une surface enveloppante fermée, aux bords idéalement continus. [↑ Figure 2 ci-dessus : Courbe fractale de Von Koch, étape n de sa construction, n tend vers l'infini.]
Précisons, si nécessaire, que l’écriture algébrique du calcul de la dimension fractale : D = (log 4) / (log 3), désigne le logarithme décimal de 4, divisé par le logarithme décimal de 3. La formule d'évaluation quantifiée de la dimension fractale D, montre intuitivement que le calcul général de la dimension fractale (indice d'irrégularité morphologique) d'une configuration géométrique générée par un algorithme déterministe (tel celui de la courbe de Von Koch, celui de la courbe de Peano ou, entre autres, celui de l'ensemble triadique de Cantor), met en rapport le logarithme (décimal ou népérien) du nombre d'éléments N obtenus après application de l'opérateur de fractionnement du « tout » initial (ici : N = 4), divisé par le logarithme de l'inverse F de l'opérateur de fractionnement 1/F (ici : F = 3, puisque l'opérateur de fractionnement 1/F = 1/3). D'où la formule générale de calcul de la dimension D des fractals scalants :
D = (log N / log F) = log N × (1 / log F)
– Rappel : le logarithme décimal d’un nombre N est la puissance n, entière ou décimale, à laquelle il faut élever le nombre 10 pour calculer N, soit : N = 10n.
4. Dimension fractale de la « courbe remplissante » de Peano
 La courbe fractale du mathématicien italien Giuseppe Peano (1858-1932) – connu également pour son axiomatisation des fondements de l'arithmétique –, dite « courbe remplissante » (1890), est un exemple-type de configuration géométrique dont la dimension fractale est égale à la dimension topologique qui est celle d'une surface plane, soit D = 2. En effet, cette courbe construite algébriquement par Peano en 1890, remplit complètement un carré [0 × 1] × [0 × 1] en passant ad infinitum par tous les points de coordonnées rectangulaires (a, b) de ce carré, qui forment un ensemble de points défini dans R² infiniment dense (c'est-à-dire un ensemble infini non dénombrable). C'est pourquoi une telle courbe est dénommée « courbe remplissante », puisqu'elle remplit intégralement l'aire d'un carré de dimension topologique (euclidienne) D = 2. Sa dimension fractale scalante : D = (log 9 / log 3) = 2, est, en théorie, exactement égale à la dimension topologique
La courbe fractale du mathématicien italien Giuseppe Peano (1858-1932) – connu également pour son axiomatisation des fondements de l'arithmétique –, dite « courbe remplissante » (1890), est un exemple-type de configuration géométrique dont la dimension fractale est égale à la dimension topologique qui est celle d'une surface plane, soit D = 2. En effet, cette courbe construite algébriquement par Peano en 1890, remplit complètement un carré [0 × 1] × [0 × 1] en passant ad infinitum par tous les points de coordonnées rectangulaires (a, b) de ce carré, qui forment un ensemble de points défini dans R² infiniment dense (c'est-à-dire un ensemble infini non dénombrable). C'est pourquoi une telle courbe est dénommée « courbe remplissante », puisqu'elle remplit intégralement l'aire d'un carré de dimension topologique (euclidienne) D = 2. Sa dimension fractale scalante : D = (log 9 / log 3) = 2, est, en théorie, exactement égale à la dimension topologique 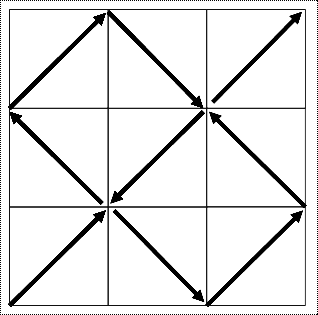 immédiatement supérieure à celle d'une droite idéalement fine, sans aucune épaisseur, de la géométrie euclidienne (D = 1) ; c'est-à-dire qu'elle correspond, mais à l'infini – sa construction fonctionnelle ne pouvant jamais être exhaustivement achevée –, à la dimension topologique classique d'une surface plane elle-même sans aucune épaisseur (D = 2).
immédiatement supérieure à celle d'une droite idéalement fine, sans aucune épaisseur, de la géométrie euclidienne (D = 1) ; c'est-à-dire qu'elle correspond, mais à l'infini – sa construction fonctionnelle ne pouvant jamais être exhaustivement achevée –, à la dimension topologique classique d'une surface plane elle-même sans aucune épaisseur (D = 2).
[↑ Figure 3 ci-dessus : Courbe de Peano, Carré de base et diagonale génératrice. / → Figure 4 ci-contre : Courbe de Peano, 1è itération.]
L'algorithme de génération itérative d'une courbe remplissante de Peano est relativement simple à énoncer en quelques instructions :
a) L'élément géométrique initial de base est un carré dont l'aire est l'ensemble hyperdense (continu non dénombrable) des points (a, b) dans R² : [0 × 1] × [0 × 1].
b) L'élément générateur est la diagonale du carré – de longueur « unité » par définition –, munie de l'opérateur de réduction homothétique : 1/3.
1. Le carré de base est subdivisé en 3 × 3 = 9 mini-carrés.
2. Les 9 diagonales des 9 petits carrés sont tracées successivement en formant une ligne continue, en partant du premier carré situé en bas à gauche. On constate que chacune des 9 diagonales qui traversent chacun des 9 mini-carrés a une longueur égale au 1/3 de la diagonale du carré initial de base. Le rapport 1/3 est le facteur de réduction homothétique de la diagonale génératrice de longueur unité, et ce facteur de réduction produit 9 mini-diagonales, chacune d'entre elles étant de longueur égale au tiers de la diagonale génératrice initiale. [↑ Figure 5 ci-dessus : Courbe de Peano, Générateur en vue redressée verticale de la Figure 4 ci-dessus.]
Le processus de construction de la courbe remplissante est ensuite itéré indéfiniment : chacun des 9 mini-carrés est à son tour subdivisé en 9 autres mini-carrés, traversés par leur diagonale respective, dont la longueur est égale au 1/3 de la diagonale de chaque mini-carré initial. Toutes les diagonales mises bout à bout dans le même ordre, en 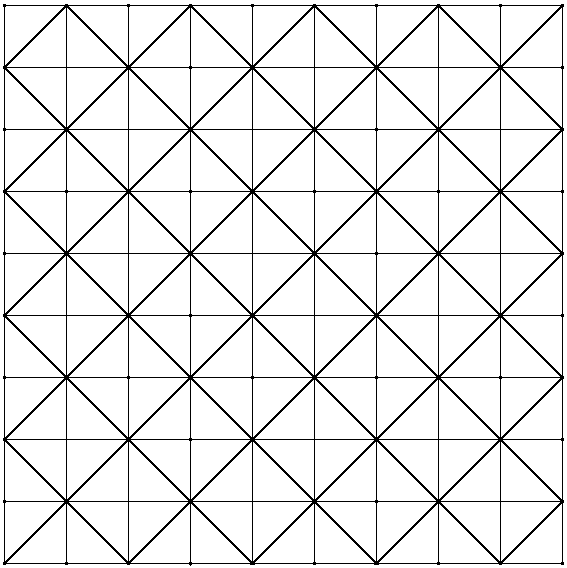 partant du premier carré situé en bas à gauche et sans jamais recouvrir une même diagonale, forment une courbe continue entre elles, qui « remplit » progressivement l'intégralité de l'aire du grand carré de départ. Tout comme la courbe fractale en flocon de neige de Von Koch, sa longueur est théoriquement infinie, bien qu'elle soit contenue dans une aire bornée de l'espace R² : [0 × 1] × [0 × 1].
partant du premier carré situé en bas à gauche et sans jamais recouvrir une même diagonale, forment une courbe continue entre elles, qui « remplit » progressivement l'intégralité de l'aire du grand carré de départ. Tout comme la courbe fractale en flocon de neige de Von Koch, sa longueur est théoriquement infinie, bien qu'elle soit contenue dans une aire bornée de l'espace R² : [0 × 1] × [0 × 1].
En vertu de la règle de calcul de la dimension fractale, expliquée à la fin du paragraphe précédent concernant la courbe de Von Koch – Cf. § 3 ci-dessus : Dimension fractale de la courbe de Von Koch –, la dimension fractale de la courbe remplissante de Peano vaut : D = (log 9 / log 3) = 2, qui correspond en fait à la dimension topologique euclidienne de l'aire du carré. Stricto sensu, la courbe enveloppante de Peano, en tant qu'objet mathématique idéal, autrement dit réalisé en théorie « à l'infini », n'est donc pas vraiment un objet fractal mais un objet géométrique euclidien,appartenant au registre topologique des dimensions entières (ici, D = 2). [↑ Figure 6 ci-dessus : Courbe de Peano, Nième itération, N tend vers l'infini.]
En revanche, considérée en tant qu'objet géométrique fonctionnellement construit par itération ad infinitum (comme le « flocon de neige » de Von Koch, parmi une infinité potentielle d'exemples de fractals scalants), donc en tant qu'objet géométrique indéfiniment approché, elle constitue bien un objet fractal dont la dimension fractale (1 < D < 2) tend indéfiniment vers la dimension topologique entière D = 2. Autrement formulé : D ≈ 2 ou D infiniment proche de 2, la différence en valeur absolue : (2 − D), étant aussi voisine de zéro que l'on voudra arbitrairement, en fonction du nombre d'étapes, aussi grand que l'on veut a priori, de la construction itérative de la courbe remplissante.
© Jean-Claude Chirollet