Point euclidien / Point fractal
1. Le concept de point euclidien
En géométrie euclidienne, le point est mathématiquement défini comme un néant physique, une absence complète de matérialité, le Rien ou le Zéro. Le point géométrique ne possède aucun attribut matériel : ni granulosité, ni couleur, ni irrégularité graphique ; il est indivisible et sans aucune figure particulière. C’est en quelque sorte le fragment absolu, idéal, au-delà duquel la pensée ne peut plus imposer ses divisions, ses fractionnements opératoires. Dans son livre intitulé Point et ligne sur plan, le peintre russe et théoricien de l'art Wassily Kandinsky (1866-1944) commence d’ailleurs par là sa réflexion : « Le point géométrique est un être invisible. Il doit donc être défini comme immatériel. Du point de vue matériel, le point égale Zéro. /…/ En pensée abstraite ou dans notre conception, le point est idéalement petit, idéalement rond. En somme, il est le cercle idéalement petit. » (Wassily Kandinsky, Point et ligne sur plan, 1926, traduction de l'allemand Paris, Éditions Gallimard, coll. folio/essais, p. 25 et p. 33, 1991).
Le peintre suisse et théoricien de l'art de langue allemande Paul Klee (1879-1940), professeur au Bauhaus de Weimar comme Kandinsky, exprima cette conception abstraite du point géométrique en termes analogues, définissant le point géométrique comme « être-néant » ou « néant-être » (Paul Klee, "Note sur le point gris", 1921-1922, in Théorie de l’art moderne, traduction de l’allemand Paris, Éditions Denoël, coll. folio/essais, 1985). L’origine de la conception du point comme entité géométrique idéale, se trouve dans les Éléments d’Euclide, mathématicien grec de l’Antiquité (Alexandrie, vers 325-265 avant J.-C).
La toute première définition du Livre premier des Éléments (traité de mathématique composé de treize livres, dont Euclide ne fut sans doute pas l'unique auteur), énonce cette définiton, purement négative, du point mathématique : « Un point (sêméion) est ce qui n’a aucune partie » (Ʃημεϊόν έστιν, ού μέρος ούθέν.). Le terme grec « sêméion » (Ʃημεϊόν) utilisé pour désigner le point mathématique, signifie littéralement le « signe », entité idéale sans figure. Le point euclidien n’ayant aucune partie, il n’a donc ni longueur, ni largeur, ni épaisseur ; il n’est donc pas une grandeur, et n’est par conséquent pas mesurable. En langage mathématique moderne, le concept de point réfère à l'idée d'élément géométrique « infiniment petit » indivisible. En effet, la mesure des grandeurs (qui s’exprime par les rapports qu’elles ont entre elles) implique leur divisibilité en parties distinctes.
Cependant, le point mathématique – élément idéal indivisible, infiniment petit et sans figure – constitue l’élément primitif de la géométrie. La définition du point par Euclide peut aussi se traduire en termes équivalents : « Un point est ce dont la partie est nulle ». Ce qui revient à dire que c’est un néant de figure, une entité abstraite sans aucune partie, donc idéalement indivisible. Sa dimension géométrique (topologique) est donc, selon la définition euclidienne, absolument égale à zéro. Le point mathématique euclidien représente, à ce titre, la fragmentation ultime de la pensée, l’objectité absolue du fragmentaire, indépendamment de toute intuition sensible qui pourrait encore donner à la notion de « point » un quelconque substrat phénoménal.
Cependant, le point euclidien représente une sorte d’archétype ou de virtualité de tous les points matériels, en nombre infini,que les artistes peuvent créer empiriquement, éventuellement par le moyen de la numérisation séquentielle des images (la pixellisation). Le point géométrique sous-tend, idéalement, la production et la perception esthétique des innombrables exemples de points picturaux, mis en œuvre par les artistes dans leurs compositions. C’est bien là le sens que Wassily Kandinsky et Paul Klee donnaient au concept de point, sous l’angle de son universalité immatérielle, définissable mais non représentable, bien que – et pour cette raison – génératrice, à la manière d’un moteur secret, de figures visuelles polymorphes à l’infini. Selon la terminologie de Kandinsky dans Point et ligne sur plan (1926), le point géométrique idéal (euclidien) est le point « intérieur » du point pictural concret matériel, polymorphe, lequel est le point « extérieur » ou l’extériorisation du premier. Le fragment « en soi », absolu, qu’est le point euclidien idéal, désigne dans ce contexte artistique le principe ou l'archétype générateur de la multiplicité des fragments matériels « relatifs », concrétisables par l’art.
Le Livre premier des Éléments d'Euclide comporte, dès son introduction, une liste de vingt-trois définitions (suivie de cinq postulats et dix axiomes) qui constituent la base élémentaire des démonstrations ultérieures contenues dans le traité de géométrie. Les deux éléments fondamentaux que sont le point et la ligne sont conçus et définis dans leur idéalité absolue, c'est-à-dire en tant que formes abstraites originaires, génératrices de toutes les figures du plan. Les éléments premiers euclidiens, par la force de leur abstraction conceptuelle, ont servi et continuent de servir puissamment la complexification continue de la mathématique classique depuis l'Antiquité grecque, ainsi que la construction des théories physiques et leurs applications. Mais ils nous permettent aussi de mesurer la distance de pensée qui s'est instaurée entre la géométrie euclidienne (standard) et la géométrie fractale (non-standard).
Définitions 1 à 7 du Livre premier des Éléments d'Euclide :
1) Un point est ce qui n'a aucune partie [= infiniment petit indivisible, immatériel].
2) Une ligne est une longueur sans largeur [= une unique dimension].
3) Les extrémités d'une ligne sont des points.
4) Une droite est une ligne dont l'extension entre deux quelconques de ses points, est
égale à la distance entre ces points.
5) Une surface est ce qui possède longueur et largeur seulement.
6) Les extrémités d'une surface [= ses bords, ses limites] sont des lignes.
7) Un plan est une surface dont l'extension entre deux quelconques de ses droites, est
égale à la surface comprise entre ces droites.
Ci-joint (fichier pdf) le début du Livre I des Éléments d'Euclide (Définitions, Postulats, Axiomes), texte grec et traduction française :
 Euclide, Eléments Livre I, Definitions, Postulats, Axiomes
Euclide, Eléments Livre I, Definitions, Postulats, Axiomes
En résumé, dans l'axiomatique euclidienne, le point a la dimension entière D = 0, la ligne a la dimension entière D = 1, et le plan (la surface) possède la dimension entière D = 2. Quant au solide (volume), il possède la dimension D = 3 en géométrie euclidienne, car il relie entre eux des points, des lignes − courbes ou droites − et des plans, tous éléments ayant des dimensions entières. Il n'existe aucun intermédiaire fractionnaire entre ces dimensions géométriques entières : 0, 1, 2 et 3.
2. Du point euclidien à la « poussière de points » fractale de Cantor
Georg Cantor étudia en 1883 cet étrange objet mathématique : « l'ensemble triadique », baptisé également du nom évocateur de « poussière de Cantor ». Il s'agit d'un ensemble fractal de points infinitésimaux, généré à partir d’un segment de droite [AB] de longueur finie, sur l’intervalle fermé à valeurs réelles infinies non-dénombrables [0, 1]. − Rappelons, à ce propos, que l’ensemble des nombres réels sur l’intervalle fermé [0, 1] est infini non dénombrable, car il est équipotent à l’ensemble R des nombres réels tout entier. Il y a en effet autant de « points » dans l’intervalle [0, 1] que dans l’ensemble R tout entier. Le microsegment [0, 1] contient donc virtuellement, en quelque sorte, l'intégralité du macro-univers infiniment dense des nombres réels, répartis de manière ordonnée sur une ligne imaginaire continue, de longueur infinie, sans commencement ni fin.
Le générateur fractal de l'ensemble triadique de Cantor, indéfiniment répétitif, est plutôt simple : le segment de droite [AB] est découpé en 3 parties, égales à 1/3 chacune de la longueur totale [0, 1]. Le tiers médian est supprimé, seuls sont conservés les deux tiers latéraux. À cette première étape du générateur, il reste donc 2 segments (21) de longueur 1/3. L’opération de fragmentation est ensuite réitérée pour les tiers restants : à la deuxième étape, il reste 4 segments (22) de longueur égale à 1/32 = 1/9. Puis la fragmentation est réitérée à l’identique pour les segments restants : à la troisième étape, il reste 8 segments (23) de longueur égale à 1/33 = 1/27.
La fragmentation se poursuit en théorie indéfiniment. À la nè étape, il reste 2n segments de longueur égale à 1/3n, pour n aussi grand que l’on veut. Quand n « tend vers l’infini » (n → ∞), 1/3n tend vers 0, c’est-à-dire est extrêmement voisin de zéro, ou encore « approximativement égal » à zéro (1/3n ≈ 0). En poursuivant le raisonnement « à l'infini », il ne subsiste plus qu'une « poussière de points » infinitésimaux, dont la dimension fractale : D = (log 2 / log 3) = 0,6309…, est intermédiaire entre la dimension topologique du point (D = 0) et celle de la ligne idéalement continue (D = 1), alors que le segment initial a pourtant été pulvérisé une infinité de fois.
La « poussière de points » – ou ensemble triadique – de Cantor, c’est précisément l’ensemble potentiellement infini des microsegments restants, obtenus par itérations successives ad infinitum, dont la somme : 2n/3n, est voisine de zéro (2n/3n ≈ 0 puisque 3n croît beaucoup plus vite que 2n), alors qu’il y a une infinité potentielle de microsegments ! Il s'agit par conséquent d'un ensemble infini non dénombrable d'éléments, mais de mesure topologique « négligeable », selon l'expression mathématique consacrée. Ci-dessous une représentation des étapes 1 à 7 de sa construction géométrique, le nombre d'étapes réel n tendant vers l'infini (n → ∞).
Cliquez sur l'image !
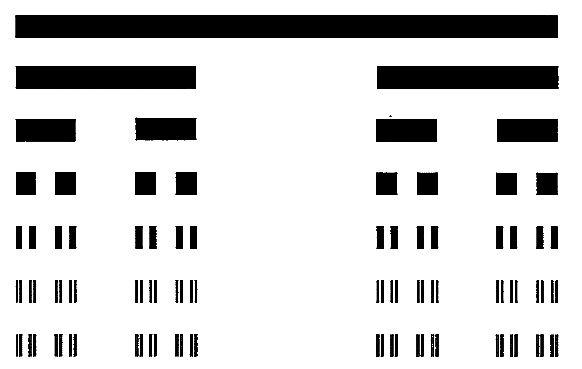 En langage mathématique non-standard, l’ensemble triadique de Cantor (de dimension fractale D = log 2 / log 3 ≈ 0,63) est une « poussière de points » infinitésimaux, en nombre infiniment grand quand n = ω-ig. [où ω-ig signifie : le nombre ω ("oméga") est infiniment grand mais toujours fini]. Il s'agit là typiquement d'un ensemble dénommé ensemble « intermittent » en physique du chaos. Chaque microfragment unitaire (ou « point » fractal) de l’ensemble triadique, quelle que soit son échelle de grandeur intermédiaire (ou mésoscopique), a donc une valeur numérique extrêmement proche de zéro, mais non nulle (1/3ω ≈ 0). Par exemple, dans l'ordre des puissances algébriques croissantes, un « point » cantorien de longueur 1/3ω (ω-ig), obtenu par l'itération indéfinie du générateur triadique, possède une dimension géométrique supérieure à celle d’un point de dimension (1/3ω)2, et à plus forte raison supérieure à celle d’un point de grandeur (1/3ω)ω, etc. Les ordres de grandeurs dans l'univers des nombres infiniment petits pourraient être énoncés indéfiniment, pour l'éternité, à la manière d'une mise en abyme de micro-poupées gigognes.
En langage mathématique non-standard, l’ensemble triadique de Cantor (de dimension fractale D = log 2 / log 3 ≈ 0,63) est une « poussière de points » infinitésimaux, en nombre infiniment grand quand n = ω-ig. [où ω-ig signifie : le nombre ω ("oméga") est infiniment grand mais toujours fini]. Il s'agit là typiquement d'un ensemble dénommé ensemble « intermittent » en physique du chaos. Chaque microfragment unitaire (ou « point » fractal) de l’ensemble triadique, quelle que soit son échelle de grandeur intermédiaire (ou mésoscopique), a donc une valeur numérique extrêmement proche de zéro, mais non nulle (1/3ω ≈ 0). Par exemple, dans l'ordre des puissances algébriques croissantes, un « point » cantorien de longueur 1/3ω (ω-ig), obtenu par l'itération indéfinie du générateur triadique, possède une dimension géométrique supérieure à celle d’un point de dimension (1/3ω)2, et à plus forte raison supérieure à celle d’un point de grandeur (1/3ω)ω, etc. Les ordres de grandeurs dans l'univers des nombres infiniment petits pourraient être énoncés indéfiniment, pour l'éternité, à la manière d'une mise en abyme de micro-poupées gigognes.
L'idée du point fractal cantorien n'est donc pas identique, conceptuellement, à celle du point topologique euclidien de dimension nulle (D = 0). Le point fractal cantorien, intermédiaire entre 0 et 1 (D = 0,6309...), est en quelque sorte un « quasi-rien » indéfiniment divisible, et l’ensemble potentiellement infini de tous les microsegments infinitésimaux, est lui-même de dimension voisine de zéro, mais non nulle. Pour cette raison, l'ensemble triadique de Cantor est dit « négligeable » puisque voisin de zéro, bien qu'étant infini non dénombrable.
On peut appliquer d’autres générateurs fractals que le classique générateur triadique − notamment des générateurs aléatoires −, engendrant d’autres ensembles fractals de Cantor, mais possédant tous une dimension fractale D comprise entre 0 et 1, intermédiaire entre le point euclidien « zéro-dimensionnel », et la ligne euclidienne idéalement mince, figure abstraite constituée de points en nombre infini, sans aucune épaisseur (D = 1).
En résumé : l'algorithme itératif de construction de la « poussière fractale » cantorienne pulvérise la ligne droite finie [AB] définie dans l'intervalle fermé à valeurs réelles [0, 1], en une infinité de micropoints, correspondant eux-mêmes à une infinité (potentielle) d’échelles de grandeurs infiniment petites, de telle sorte qu’il engendre, paradoxalement, la vacuité quasi totale avec du trop-plein, avec de l’excès, avec l’infini même, en quelque sorte. L'idée de point fractal retrouve par là-même une certaine forme de connotation intuitive, éliminée par la définition euclidienne du point sans partie, de dimension nulle.
3. L'ensemble fractal de Cantor : un univers de nombres non-archimédiens
Le point fractal − l'appellation « point » est conventionnelle − infiniment petit non nul s’inscrit, de ce fait, dans un système géométrique de nombres non-archimédiens. Il s’agit là d’une propriété qui découle de l’usage des nombres hyperréels non-standards, infiniment petits non nuls (ε-ip) et infiniment grands mais finis (ω-ig). Ainsi, pour reprendre les trois ordres de grandeurs infinitésimales évoqués ci-dessus, par ordres de grandeur décroissants, entre les « points » d’ordre 1/3ω, (1/3ω)2 et (1/3ω)ω (ω : infiniment grand d'ordre 1), il n’existe pas de passage progressif et continu, seulement des sauts, des ruptures, des discontinuités d’ordres de grandeurs, qui agissent comme des loupes de grossissement, des zooms discontinus sur des fragments géométriques indétectables dans un ordre inférieur.
Le « point fractal » n’est pas une donnée géométrique dernière et indivisible. Il requiert, pour sa définition opératoire, une succession illimitée de zooms numériques sur une indéfinité d’ordres de grandeurs infiniment petites, inscrites dans un univers insondable de valeurs hyperréelles non archimédiennes, qui ne « communiquent » pas entre elles de manière progressive et continue, car elles ne sont pas commensurables. Cela signifie, par extension, que chaque « point fractal » détient en son sein une infinité de détails potentiels incommensurables, en fonction des innombrables ordres de grandeurs infinitésimaux qui peuvent être envisagés ad libitum. Il se fragmentise en une infinité potentielle de micropoints fragmentaires, toujours plus « détaillés », c’est-à-dire de plus en plus finement découpés, analysés, produisant sans fin une pléthore d'océans insondables et incommensurables entre eux, de grandeurs non- archimédiennes.
Le concept mathématique de « point fractal » cantorien ne réfère donc pas à un objet idéal unique et clos sur soi, mais à une classe d'objets idéaux en nombre infini (non dénombrables) appartenant à un même ordre de grandeur, et contenant en elle potentiellement − telles d'innombrables poupées gigognes − une infinité de classes d'objets idéaux en nombre infini, appartenant à une infinité d'ordres de grandeur inférieurs. Une telle définition fractaliste du concept de « point » détient son sens géométrique de la seule construction algébrique d'un système de nombres non-archimédiens.
© Jean-Claude Chirollet
