Arts / Numérisation / Fractals

Il existe plusieurs dizaines ou centaines de milliers d'articles et de livres concernant la théorie des fractals – sans compter les sites Internet –, écrits en toutes langues depuis les années 1970, dont un très grand nombre en anglais. Beaucoup de ces ouvrages ou articles scientifiques sont d'un niveau ultra-spécialisé, intégralement « lisibles » par seulement quelques centaines (voire moins) de mathématiciens et docteurs en mathématique dans le monde entier. D'autres, inversement, sont de la vulgarisation illustrée, compréhensible par tout individu non-mathématicien, mais intéressé cependant par certaines applications artistiques ou infographiques de ces questions. Les articles de mon blog concernant le rapport entre la science des objets fractals et l'art fractal, se situent entre la simple vulgarisation illustrée, qui ne prétendrait à rien d'autre qu'à distraire par la beauté intrinsèque des figures informatiques, et le discours purement scientifique qui n'aurait d'autre intention que celle d'exposer, de manière étendue et rigoureuse, la théorie mathématique de ces questions très complexes qui se rapportent à la géométrie des objets fractals.

→ Il est conseillé de renforcer la luminosité de l'écran, afin de révéler plus nettement les détails des images fractales, obtenues au moyen de générateurs mathématiques.

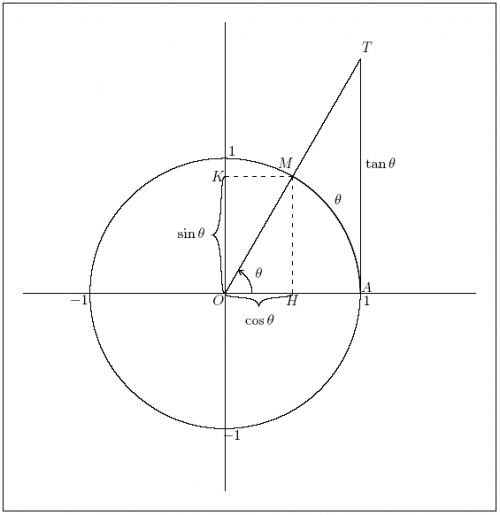La science des « objets fractals », objets mathématiques spécifiques de la géométrie non-euclidienne, inventée par le mathématicien Benoît Mandelbrot (1924-2010) dès les années 1960, a été mise à l’honneur de la littérature scientifique en 1975 dans son livre fondamental, Les Objets fractals – Forme, hasard et dimension. Cette géométrie qui s’applique aux formes irrégulières de la nature complexe, autant qu’aux figures de la mathématique pure dans le plan complexe sur 360 degrés décimaux [→ Cf. image ci-contre], ou aussi dans l'espace 3D, a servi de base de réflexion et de création aux artistes du mouvement fractaliste international depuis les années 1980, quel que soit le domaine particulier de leurs investigations artistiques respectives (arts plastiques, arts numériques, photographie, musique, voire théâtre et littérature).

Le courant artistique fractaliste regroupe la multiplicité des créations, extrêmement variées, d’artistes de différentes nationalités – Européens, Japonais, Américains –, qui ont fondé leur activité créatrice sur la référence à la théorie physico-mathématique de la complexité stochastique (c’est-à-dire aléatoire ou semi-aléaoire) des systèmes dynamiques. Or, la théorie des systèmes dynamiques, lesquels détiennent parfois une capacité « d’auto-organisation », s’édifia substantiellement au sein de la communauté scientifique internationale au cours des années 1970.

Pour le discours scientifique, la notion de complexité stochastique (ou aléatoire) implique l’idée de processus dynamiques indéterministes ou plus exactement semi-déterministes, non descriptibles par les lois ordinaires de la continuité mathématique, et par conséquent imprédictibles à long terme. Cette impossibilité de prédire leur comportement à long terme est due au fait qu’ils sont capables de s’auto-réorganiser indéfiniment de manière nouvelle au cours du temps, bien que certains systèmes auto-organisants soient, dans certains cas, quasi-prédictibles (séquence cyclique; trajectoire approchée mais globalement prédictible; etc.). Pour cette raison, ils sont donc supposés être gouvernés « objectivement » (réellement) par les seules lois du hasard. Biologistes, météorologues, sociologues, économistes, physiciens, chimistes et, bien sûr, mathématiciens, ont recours fréquemment aux « lois du hasard » pour tenter de comprendre par approximation la complexité des phénomènes imprédictibles qu’ils étudient.

En résumé, une complexité stochastique (ou aléatoire) implique effectivement des processus indéterministes, gouvernés intrinsèquement par les lois du hasard. Le grand apport des théories de la complexité a été de révéler l’existence de phénomènes simultanément déterministes et imprédictibles. Précisons enfin que les fractales mathématiques, dans cet univers complexe et imprédictible, représentent seulement l’un des aspects de ces lois du hasard, et non la seule forme qu’elles peuvent adopter.

Corrélativement, les artistes fractalistes admettent, au moins implicitement, pour modèle conceptuel présidant à la philosophie esthétique de leur entreprise créatrice, l’édifice mathématique de la géométrie fractale, formalisée par le mathématicien-informaticien Benoît Mandelbrot dans les années 1960-1970. La géométrie fractale permet, précisément, de caractériser quantitativement certaines propriétés géométriques propres à la représentation formelle des systèmes dynamiques. Le terme « fractal », utilisé comme substantif ou comme qualificatif, est par conséquent d’origine strictement scientifique, puisqu’il appartient au vocabulaire de la géométrie des phénomènes naturels – macroscopiques ou microscopiques –, infiniment irréguliers et imprévisibles en leurs détails à toute échelle d’observation. Le langage de la géométrie contemporaine dénomme donc « objet fractal » (ou plus brièvement « fractal ») une configuration spatiale à dimension non entière, qui « s’étend » dans un espace de dimension entière immédiatement supérieure, et cet espace peut posséder n’importe quel nombre de dimensions (1, 2, 3 ou n quelconque).

Cette configuration discontinue, soit apparemment très ordonnée et symétrique par changement d’échelle – par exemple, la courbe dite « flocon de neige de Von Koch », et la « courbe remplissante » de Peano, qui sont auto-identiques (scalantes) à toute échelle de grandeur –, soit très irrégulière et dissymétrique comme les côtes d’un littoral ou les contours d’un nuage, peut être caractérisée, quelle que soit l’échelle d’examen employée, par un degré d’irrégularité statistique variable que la géométrie euclidienne ordinaire ne peut mesurer et dont elle ne sait pas rendre compte de manière satisfaisante. Ce qui signifie qu’un objet fractal peut être extrêmement irrégulier, mais que ce n’est pas une condition nécessaire pour en faire un objet fractal, tandis que la mesure géométrique qui en rend compte dépend toujours de l’échelle d’examen adoptée.

À l'origine des pratiques artistiques revendiquant une appartenance esthétique fractaliste se situe donc l'étude mathématique des formes infiniment irrégulières dans leurs moindres détails, brisées, rompues et morcelées en chacune de leurs parcelles, 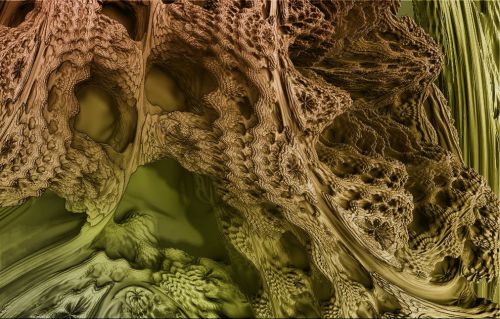donc essentiellement discontinues (le participe passé latin « fractus » résume ces acceptions qui convergent vers l'idée de moudre, de broyer et de fracturer). Le néologisme « fractal », créé par le mathématicien Benoît Mandelbrot dans la première édition française de son livre célèbre : Les Objets fractals - Forme, hasard et dimension (1^è éd. 1975; 4^è éd. revue, 1995, Paris, Flammarion), incluait également l'abandon du concept mathématique traditionnel de symétrie spatiale, liée à la géométrie euclidienne, au profit d'un autre type d'organisation régissant de manière complexe les éléments d'une configuration spatiale irrégulière en toutes ses composantes. Ce nouvel « ordre fractal » était défini en termes strictement mathématiques comme un indice algébrique d'irrégularité morphologique : la dimension fractale, nombre absolu ne désignant pas une mesure de grandeur mais une mesure de la complexité formelle des configurations planes ou tridimensionnelles. [↑ Image ci-dessus : Coupe fractale en 3D obtenue à partir d'un zoom numérique sur une mini-zone de l'ensemble de Mandelbrot calculé en 3D, dit "Mandelbulb".]

Quelles formes peuvent être considérées comme infiniment irrégulières et discontinues ? Les exemples puisés dans la nature sont omniprésents et la physique découvre qu'ils sont en extension continuelle. La structure des nuages en mouvement, la forme des montagnes, l'organisation d'un ciel étoilé, l'univers infini des galaxies, tout comme une simple feuille de châtaignier, un morceau de rocher, un fragment de métal ou une cellule biologique, humaine, animale ou végétale, sont affectés d'innombrables zones d'irrégularité en fonction des niveaux d'observation auxquels on les soumet. Le mérite de la géométrie fractale est précisément d'avoir permis de caractériser ces degrés ou niveaux d'irrégularité relative qui signent l'hétérogénéité morphostructurale de la matière et de l'univers tout entier.

Ce sont les échelles d'examen de l'objet, naturel ou géométrique, qui définissent les degrés variables de discontinuité. Le thème, bien connu en physique théorique (mécanique quantique), de l'interrelation opératoire de l'observateur avec l'objet observé, s'affirme en ce domaine mathématique comme le motif primordial de la détermination de la dimension fractale. Il existe une analogie entre les positions des observateurs en géométrie fractale et en mécanique quantique : dans les deux cas, la présence de l’observateur modifie le résultat de l’expérience en cours. Cependant, pour conserver la justesse du raisonnement, il convient de préciser que l’analogie s’arrête là : en mécanique quantique, c’est la présence même de l’observateur et de ses instruments de mesure, comme éléments de la réalité physique, qui constitue le facteur de perturbation. Dans le cas des objets fractals, le résultat est modifié selon le point de vue que l’observateur choisit de prendre : le niveau  d’échelle mésoscopique auquel il s’arrête. Les deux situations sont, pour cette raison, très différentes, et mènent donc à deux modèles du monde très différents.

Du point de vue fractaliste, les objets de la nature, observés à grande distance, peuvent apparaître globalement comme des formes simples, régulières, descriptibles au moyen des catégories de la traditionnelle géométrie euclidienne : des points (de dimension 0), des lignes (de dimension 1), des surfaces ou plans (de dimension 2), des solides (de dimensions 3), des cercles, des triangles, des parallélépipèdes, des sphères, des cônes, des cylindres, des polyèdres, et toute combinaison de ces formes élémentaires primitives. Pourtant, observées de plus près, ces formes naturelles deviennent plus compliquées, moins linéaires, moins « euclidiennes »; elles présentent des contours brisés et des structures surfaciques ramifiées, enchevêtrées. Si le niveau d'observation, toujours plus exigeant, continue de s'affiner par l'intermédiaire de la loupe et du microscope, le moindre détail apparaît alors comme une myriade de détails plus fins et toujours plus riches de microformes, elles-mêmes saturées à l'infini de microformes gigognes hyper-détaillées aux apparences nouvelles.

Bien entendu, le fractal dans la nature ne « passe pas » à l’infini. Il existe un niveau d’échelle limite dans la nature à cet aspect fractal : celui-ci s’éteint au moment où l’autosimilarité cesse. Pour un objet comme un rocher, elle cesse lorsque l’on passe au niveau des molécules, qui n’ont aucune autosimilarité formelle avec le rocher lui-même.  Le qualificatif « fractal » ne saurait donc être employé comme synonyme de « décomposable à l’infini », terminologie qui relève plus de l’acception « perceptuelle » du terme, que de son acception scientifique proprement dite.

Mathématiquement, le corollaire de l'affinement de l'échelle d'observation réside dans le fait qu'aucune symétrie euclidienne connue n'est détectable en chaque fragment étudié. Les multiples niveaux mésoscopiques de la description, virtuellement infinis, ne semblent plus pouvoir être mis en corrélation hiérarchique continue, de même que les lois de la symétrie qui caractérisent généralement un objet dans sa totalité ne semblent plus pouvoir se révéler à travers les parcellisations de l'ensemble primitif. Tout fragment se manifeste comme une nouvelle totalité, en apparence (c’est-à-dire selon le point de vue adopté) étrangère morphographiquement à l'ensemble dont est extrait le détail.

Mais un même ensemble fractal recèle en tous ses détails une parenté structurale définie par son unique mesure dimensionnelle. La loi d'unité morphologique reliant l’ensemble fractal choisi par « l’observateur » et ses parties n’est donc aucunement frappée de caducité, bien que l’aspect perceptuel de ces détails soit toujours différencié et indéfiniment varié, sous l’effet du jeu systématique des variations d'échelles d'examen.

Dans la nature physique, cependant, les niveaux d’observation ne sont pas infinis, à la différence d’un fractal mathématique, abstraction géométrique sans contrepartie dans le réel. Les physiciens et mathématiciens distinguent, parmi les objets naturels ou géométriques, les multifractals (ou hyperfractals), c'est-à-dire les objets fractals statistiquement autosimilaires — qui comportent donc des différences de détail morphologique entre eux, éventuellement à un iota près ou bien à une transformation topologique près —, des fractals simples ou scalants, c'est-à-dire purement déterministes, strictement auto-identiques : objets fractals géométriques dont la structure formelle demeure rigoureusement identique, par réplication à toute échelle de grandeur (propriété d'autosimilitude à ne pas confondre avec celle d'autosimilarité des fractals aléatoires ou semi-déterministes).

Les fractals purement déterministes sont régis par une loi dite d'homothétie interne. On dit aussi que ces fractals géométriques sont « scalants » car ils résultent les uns des autres, par transformations affines en cascade ad infinitum, sur le modèle du célèbre « flocon de neige » fractal du mathématicien suédois Helge Von Koch (1870-1924), parmi une infinité d’autres modèles possibles – notamment la fameuse « courbe remplissante » du mathématicien italien Giuseppe Peano (1858-1932), ou encore, parmi les fractals géométriques les plus connus, le tapis fractal du mathématicien polonais Waclaw Sierpinski (1882-1969).

Citons enfin, pour le plaisir de la méditation, ce beau passage écrit en 1980 par le philosophe Michel Serres faisant l’éloge de la géométrie fractale qui nous apprend à regarder le monde visible sans a priori conceptuel, sans idéalisation préconçue : « Sortons, laissons-nous conduire par Benoît Mandelbrot. Le monde terraqué nous revient, grâce à lui, par immenses morceaux, le vent, l’océan, le rivage. Ce sera bientôt la fête du monde ou le retour de l’oublié. [...] Voici le retour des éponges, naguère méprisées. » (Michel Serres, Hermès V – Le Passage du Nord-Ouest, Paris, Éd. de Minuit, 1980, p. 101 et p. 103).

[Le qualificatif « terraqué » est un terme ancien qui signifie : composé de terre et d'eau, en parlant du globe terrestre.]

© Jean-Claude Chirollet

- Texte adapté de mon article : L’approche de l’art d’un point de vue fractaliste, Jean-Claude Chirollet, revue Tangence, numéro 69, été 2002, Université du Québec, p. 103-132. — Cf. le lien PDF ci-dessous vers l'article intégral en ligne.  

 Tangence 69_2002

Cf. également :

- Jean-Claude Chirollet, Art fractaliste. La complexité du regard, Éditions L’Harmattan, collection Champs Visuels, Paris, 2005 (269 pages, 62 illustrations artistiques).

- Jean-Claude Chirollet, La question du détail et l'art fractal (à bâtons rompus avec Carlos Ginzburg), Éditions L’Harmattan, collection Histoires et idées des Arts, Paris, 2011 (278 pages, 15 illustrations artistiques).