Arts / Numérisation / Fractals

Le langage de la mathématique moderne évoque « l'axiome de continuité » à propos, en particulier, de la Définition 4 du Livre V et de la Proposition 1 du Livre X, mais aussi plus généralement du Livre XII des Éléments d'Euclide, trois livres particulièrement importants en ce qui concerne la théorie des proportions entre grandeurs géométriques de même nature : lignes, surfaces ou solides − le point, de dimension zéro, n'étant pas considéré comme une grandeur dans l'édifice de la géométrie euclidienne −, et définissant les principes fondamentaux d'une science de la mesure de ces grandeurs comparées entre elles.

Il est quasi certain que les livres V et XII des Éléments, relatifs à la théorie des proportions entre grandeurs, sont dûs à Eudoxe de Cnide (vers 408-355 avant J.-C.), astronome, géomètre et philosophe Grec. Dans son traité sur La Mesure du Cercle, Archimède de Syracuse (vers 287-212 avant J.-C.) se réfèrera explicitement à la théorie eudoxienne des proportions entre grandeurs géométriques, telle qu'elle fut formulée dans les Éléments, pour calculer par approximation polygonale la circonférence du cercle. Il s'agissait pour Archimède d'approximer au plus juste la valeur du périmètre du cercle, au moyen de l'addition des côtés en nombre aussi grand que possible, de polygones réguliers inscrits dans le cercle ou circonscrits.

Pour Eudoxe comme pour Archimède, les mathématiques sont pensées essentiellement comme la science de la mesure des grandeurs, et non comme la science des corps de nombres abstraits, considérés à travers leurs propriétés autonomes, comme c'est le cas en mathématique moderne : entiers naturels N, entiers relatifs Z, nombres rationnels Q, nombres réels R : naturels, rationnels, irrationnels et transcendants, nombres complexes C, quaternions ou « hypercomplexes » H, etc.

L'idée de la possibilité d'approximation indéfinie mais opératoirement finie, d'une mesure de grandeur par une mesure équivalente, par exemple, celle d'une circonférence par une somme de côtés polygonaux très petits, repose sur le principe rationnel de la nécessité logique d'une continuité géométrique entre le polygone à un nombre de côtés innombrables (c'est-à-dire « tendant vers l'infini », en langage mathématique standard), et le périmètre d'un disque idéalement (absolument) circulaire. Leibniz (1646-1716), à la fin du dix-septième siècle (publication de 1684), qualifiait ce polygone à une infinité potentielle de côtés infinitésimaux, assimilable à un cercle parfait, de « polygone infinitangle », c’est-à-dire, littéralement, un polygone ayant une infinité d’angles obtus tendant indéfiniment vers l’angle plat (180 degrés décimaux).

L'histoire des mathématiques évoque la « méthode d'exhaustion » eudoxienne ou euclidienne, car il s'agit, dans l'idéal, d'épuiser ou de réaliser exhaustivement le processus d'approximation des grandeurs jusqu'à son terme ultime − sous-entendu : par passage à la limite à l'infini, dans le langage de l'analyse classique des limites, depuis les travaux en ce domaine de Bernard Bolzano (1781-1848), d'Augustin-Louis Cauchy (1789-1857) et surtout ceux de Karl Weierstrass (1815-1897).

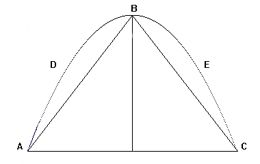
     Approximation indéfinie de la mesure du cercle par la 

    méthode des polygones réguliers inscrits et circonscrits (le 

    nombre des côtés polygonaux tend en théorie vers l'infini).

Ce que la mathématique moderne dénomme « axiome de continuité », depuis la création, dans la seconde moitié du dix-neuvième siècle, de la théorie de ensembles de Georg Cantor (1845-1918) et Richard Dedekind (1831-1916), c'est précisément le principe de commensurabilité des grandeurs homogènes entre elles (des lignes entre elles, des surfaces entre elles, des solides entre eux, et aussi pour Archimède des temps entre eux), autrement dit le fait que ces grandeurs A et B puissent être comparées entre elles et mesurées au sein d'un système de mesure de référence. Par exemple : B = (n × A) où B et A représentent des grandeurs linéaires exprimées en millimètres, et n représente un nombre entier ou un nombre décimal supérieur ou inférieur à 1. La mesure comparée des deux grandeurs peut alors se traduire par le rapport arithmétique A/B ou B/A, en vertu de l'axiome d'Eudoxe-Archimède, plus brièvement appelé « axiome d'Archimède » (ou « lemme d'Archimède ») dans la littérature mathématique, puisque Archimède a repris à son compte dans ses démonstrations géométriques, et plusieurs fois évoqué cet axiome eudoxien de la géométrie d'Euclide.

Voici certaines formulations de l'axiome d'Eudoxe-Archimède (dit « axiome de continuité » en mathématique cantorienne), dans les Éléments d'Euclide :

Livre V, Définitions 1, 2, 3, 4 et 6 des Éléments d'Euclide :

Définition 1 :

« On appelle sous-multiple ou partie aliquote (une part) d'une grandeur, sa partie la plus petite, quand celle-ci (prise comme unité) mesure la partie la plus grande. » (Euclide, Éléments, texte grec et traduction française de Georges J. Kayas, éd. du C.N.R.S., Paris, 1978, Tome I, p. 83).

Définition 2 :

« La plus grande partie est appelée multiple de la plus petite, quand elle est mesurable par cette dernière. » (ibid., Tome I, p. 83).

Définition 3 :

« On appelle rapport de deux grandeurs homogènes, la relation quantitative exprimant le nombre de fois que l'une des grandeurs est contenue dans l'autre. » (ibid., Tome I, p. 83).

Définition 4 (formulation la plus typique) :

« On dit que deux grandeurs sont dans un certain rapport entre elles, si, par multiplication, elles sont capables de se dépasser l'une l'autre. » (ibid., Tome I, p. 83).

Définition 6 (la définition 5 est implicitement contenue dans celle-ci) :

« Les grandeurs qui sont dans le même rapport entre elles sont appelées grandeurs proportionnelles. » (ibid., Tome I, p. 83).

Livre X, Proposition 1 des  Éléments d'Euclide :

« Étant données deux grandeurs inégales, si de la plus grande on retranche plus que sa moitié, puis du reste ainsi obtenu on retranche encore plus que sa moitié, et si l'on continue toujours ainsi, nous aboutirons finalement à une grandeur qui est inférieure à la plus petite des grandeurs données. » (ibid., Tome II, p. 69).

Le raisonnement opératoire exposé dans cette Proposition 1 du Livre X des Éléments d'Euclide est traditionnellement appelé « antiphérèse » ou algorithme d'Euclide. Il est symétrique, logiquement, de la Définition 4 du Livre V, énoncée ci-dessus. Ces énoncés euclidiens supposent une homogénéité absolue des sortes de grandeurs mises en rapport, condition sine qua non du principe de commensurabilité des grandeurs entre elles (lignes/surfaces/solides/et temps chez Archimède). C'est précisément ce que signifie l'expression « être dans un certain rapport » (ou encore « avoir raison commune ») dans les Définitions 4 et 6 du Livre V, par exemple.

Voici à présent la formulation de l'axiome de continuité par Archimède, dans l'introduction de La Quadrature de la Parabole, où Archimède fait implicitement référence à la Définition 4 du Livre V des Éléments d'Euclide – même si, par ailleurs, il considère que les démonstrations géométriques des théorèmes qui présupposèrent cet axiome auraient pu, éventuellement, s'en passer.

Archimède, La Quadrature de la Parabole, Introduction :

« En ce qui concerne le segment compris entre une droite et une parabole, nous savons qu'aucun des géomètres anciens n'en a cherché la quadrature, que nous avons trouvée maintenant ; nous démontrons, en effet, que tout segment compris entre une droite et une parabole est équivalent aux quatre tiers du triangle ayant même base et même hauteur que le segment, en admettant pour la démonstration le lemme que voici : l'excès de la plus grande de deux aires inégales sur la plus petite peut dépasser, s'il est ajouté (sc. un nombre suffisant de fois) à lui même, toute aire finie donnée. Or les géomètres antérieurs ont fait appel eux aussi à ce lemme ; car c'est en se servant de ce lemme qu'ils ont démontré que les cercles ont entre eux le rapport des carrés sur leurs diamètres et que les sphères ont entre elles le rapport des 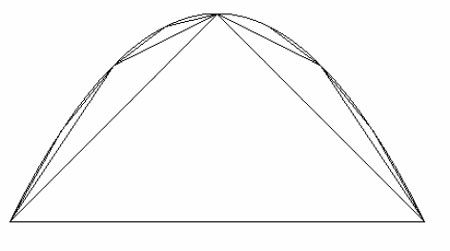cubes sur leurs diamètres (...). Il se trouve cependant que tous ces  théorèmes cités sont considérés comme non moins vrais que ceux qui ont été démontrés sans ce lemme (...) »  (Archimède, La Quadrature de la Parabole, Texte grec établi et traduit par Charles Mugler, Paris, Société d'Édition « Les Belles Lettres », 1971, p. 164-165).  

– Note : dans la traduction de Charles Mugler, « sc. » est l'abréviation du latin : « scilicet » qui signifie : à savoir, c'est-à-dire, sans doute, évidemment, il va sans dire, etc., pour indiquer une idée évidente ou une explication sous-entendue qui s'impose logiquement, non explicitées par l'auteur.

Ci-joint (fichier pdf) l'introduction de La Quadrature de la Parabole d'Archimède, texte grec et traduction française par Charles Muller, Paris, Société d'Édition « Les Belles Lettres », 1971, p. 164-165 :

 Archimède_Quadrature de la Parabole_Lemme de Continuité 

Trois conséquences logiques découlent de cette théorie de la commensurabilité :

1. En vertu de cette communauté d'espèce entre grandeurs, étant données deux grandeurs homogènes A et B, on pourra toujours déterminer sans aucune ambiguïté l'une de ces trois relations d'ordre entre elles : A < B, A = B ou A > B. On pourra également toujours établir l'équivalence des rapports de grandeurs : A/B = C/D. En particulier, si l'on a trois grandeurs données de même espèce : A, B et C, et le rapport A/B, il sera toujours possible de définir une grandeur D qui soit avec C dans le même rapport que B est à A. C'est la définition de la « quatrième proportionnelle » et plus généralement du concept de proportionnalité, dont les définitions et les propositions du Livre V des Éléments d'Euclide établissent la théorie.

2. L'axiome de continuité donne un statut mathématique négatif aux grandeurs incommensurables entre elles. Les grandeurs de même espèce étant toujours multipliables ou divisables indéfiniment (mais pas à l'infini), le résultat de l'itération opératoire ne peut pas être exprimé par un rapport de nombres entiers, car il n'est pas égal à un minimum commun à ces grandeurs divisées ou multipliées. En particulier, le point n'est pas considéré par Euclide comme le minimum ou le plus petit élément d'une suite de grandeurs décroissantes. Le point, élément géométrique zéro-dimensionnel, sans partie et donc indivisible, échappe à toute mesure puisque seuls les rapports de grandeurs sont calculables (Éléments, Livre I, Définition 1).

3. Enfin, ces rapports de grandeurs excluent toute idée d'infini et tout concept de grandeur infinitésimale, puisque les grandeurs peuvent toujours se dépasser l'une l'autre par multiplication, ou inversement devenir inférieures l'une par rapport à l'autre par division répétée. L'axiome d'Eudoxe-Archimède, sous ses deux formulations symétriques, autorise l'algorithme de divisibilité illimitée, mais sans pour autant conduire à des indivisibles infinitésimaux. Il est appliqué, par exemple, dans l'algorithme d'Euclide exposé dans la Proposition 2 du Livre X des Éléments, qui établit l'irrationnalité des grandeurs qui ne se divisent pas entre elles, ainsi que dans la Proposition 1 du Livre VII, qui définit la non-divisibilité des nombres premiers entre eux.

Reformulons à présent « à la lettre », en un langage arithmétique modernisé, l'axiome de continuité d'Eudoxe-Archimède, sous les deux formes symétriques énoncées dans les Éléments : Livre V, Définition 4 et Livre X, Proposition 1 (Cf. ci-dessus).

— Livre V, Définition 4 : soit 2 grandeurs A et B, telles que : B > A, la différence entre elles pouvant être aussi grande que l'on veut arbitrairement. A et B étant homogènes (de même espèce), il existe nécessairement un nombre entier k tel que l'inégalité kA > B soit toujours vérifiée, quelle que soit B aussi grande que l'on veut arbitrairement.

— Livre X, Proposition 1 : soit 2 grandeurs A et B, telles que : B > A, la différence entre elles pouvant être aussi grande que l'on veut arbitrairement. A et B étant homogènes (de même espèce), il existe nécessairement un nombre entier k et un nombre réel r compris entre 1/2 et 1 (1/2 < r < 1), de telle sorte que l'inégalité suivante soit toujours vérifiée : B (1 – r)^k < A, quelle que soit la grandeur A aussi petite que l'on veut arbitrairement.

Les constructions géométriques du Livre XII des Éléments – attribué avec quasi-certitude à Eudoxe – seraient impossibles sans le fondement logique implicite de l'axiome de continuité (rappelons que l'expression « axiome de continuité » n'est bien évidemment pas d'Eudoxe, Euclide ou Archimède, mais correspond à la formulation moderne de la théorie cantorienne des ensembles). Dans ce Livre XII, en effet, les calculs d'aires et de périmètres circulaires au moyen de polygones réguliers inscrits et circonscrits seraient impossibles sans la présupposition et l'application intuitive du lemme d'Eudoxe-Archimède, puisqu'il est nécessaire opératoirement de rendre la différence de grandeur entre l'aire du cercle et celle des polygones (inscrits ou circonscrits) aussi petite que l'exige la démonstration géométrique, c'est-à-dire inférieure à une grandeur donnée arbitrairement petite mais finie. Or, pour y parvenir, il faut multiplier en théorie indéfiniment, mais en pratique (opératoirement) de manière finie, le nombre de mini-côtés des polygones. Dans le Livre XII des Éléments, le problème du calcul du volume de la pyramide, du cône, du cylindre et de la sphère, se pose de manière analogue au problème concernant la mesure du cercle.

© Jean-Claude Chirollet