Arts / Numérisation / Fractals

Le texte ci-dessous concerne exclusivement les images fractales numériques (Fractales), générées au moyen d’algorithmes informatiques déterministes . L'écriture « Fractales » (au féminin, avec une lettre majuscule) est destinée à les distinguer à la fois des objets fractals purement mathématiques étudiés par le mathématicien, et des phénomènes naturels chaotiques étudiés par le physicien.

→ Il est conseillé de renforcer la luminosité de l'écran, afin de révéler plus nettement les détails des images fractales, obtenues au moyen de générateurs mathématiques.

Les Fractales numériques « fonctionnent » comme de véritables organismes logico-­informatiques, avec leur « vie » algébrique et géométrique propre, obéis­sant à une évolution typiquement chaotique, bien qu’elles soient, en leur principe, engendrées de manière déterministe (par des équations algébriques). D’où leur relative imprévisibi­lité morphologique qui les rend si curieuses, si captivantes pour le spec­tateur contemplant le renouvellement permanent des formes en couleurs sur l’écran vidéographique, fourmillement complexe dont la photographie instantanée ne peut que fournir une coupe arbitraire, mais différente de toutes celles qui ont précédé, aussi bien que de toutes celles qui suivront.

Une Fractale, c’est avant tout une forme dynamique en continuelle formation, en 2D dans le plan complexe, ou en coupe 3D créée à partir de quaternions dans l'espace complexe. [→ Image ci-contre : détail de fractale de Mandelbrot vue en coupe 3D – dite "Mandelbulb" –, créée à partir de quaternions. Cf. → Site Mandelbulb.] C’est un organisme qui se crée et se recrée continuellement, dans un renouveau de chaque fraction de seconde, à toute échelle, en tout point du plan complexe, en tout instant. Les similarités formelles ne sont jamais que localisées, ponc­tuelles ; mais similarité ne signifie pas identité d’une échelle à l’autre (pour une zone très étroite du plan), mais toujours différence absolue malgré une ressemblance formelle globale. Benoît Mandelbrot a expliqué une dif­férence très nette entre les Fractales linéaires, régies par le principe d’homo­thétie interne qui conserve la même forme quelle que soit l’échelle d’observation (le « flocon de neige » de Von Koch par exemple), et les Fractales non linéai­res, qui sont le résultat de la mise en œuvre d’un algorithme récursif, générateur de trajectoires chaotiques dans le plan ou l’espace complexe. Dans le cas des Fractales non linéaires autoréférentielles, il ne saurait exister deux zones spatiales strictement identiques, bien que des ressemblances d’ensemble soient observables à différentes échelles successives, pour une petite parcelle du plan, étudiée à des échelles de plus en plus grandes.

1. La métaphore de l’ontogenèse et du code génétique

Le processus de variation d’échelle d’exploration est essentiel dans l’émergence électronique des Fractales. Il est même la source fondamen­tale de la métaphore biologique consistant à comparer la fractalité dyna­mique de l’image et l’ontogenèse d’un être vivant à partir de son poten­tiel génétique. Car cette comparaison est très fréquemment employée par les créateurs d’images fractales, mathématiciens aussi bien que plasticiens d’ailleurs.

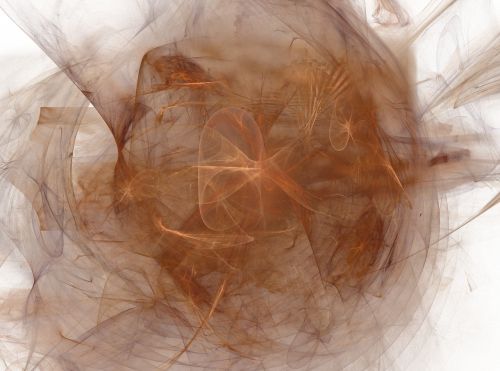Tout d’abord, il faut rappeler que la spécificité de ces images électro­niques (non réalisables à la main, car la moindre de ces belles figures complexes prendrait, selon l’expression de Mandelbrot, plusieurs centai­nes d’années pour être créée manuellement...) réside, précisément, dans le changement d’échelle généralisé et incessant, chaque variation d’échelle faisant surgir de nouveaux phénomènes visuels et de nouveaux types de trajectoires dans le plan. La récurrence fonctionnelle exerce à toute échelle d’exploration sa puissance de création de nouvelles formes imprévisibles et luxuriantes à l’infini. Des zooms dont le facteur d’échelle est très élevé peuvent être réalisés grâce à de puissants ordinateurs graphiques. Avec l’aide de ces moyens logiciels, on obtient des facteurs d’échelle extrêmement importants. Une cascade de détails est ainsi engendrée, avec également des effets de relief et de protubérances, ou des effets de voile vaporeux, diaphanes, de semi-transparence, avec des nuances chromatiques subtiles, mêlant pseudo-continuité des lignes et multiplication de nuances diamorphiques (comme la fractale dynamique ci-dessus).

Il demeure cependant évident que les couples (a,b) de nombres réels défi­nissant les points du plan dans un repère orthonormé, sont théoriquement infiniment denses et inépuisables en fait, tout comme le sont les points géométriques d’une ligne droite ou courbe, aussi courte soit-elle. Mais les variations d’échelles d’exploration topographique permettent, pour une micro-zone précise, de rétablir une sorte de continuité morphologique des formes. En passant par des échelles microscopiques de plus en plus fines, les détails inexplorés antérieurement se révèlent jusqu’à leur finesse maxi­male pour une échelle donnée.

Comme dans un organisme vivant, à toute échelle se révèlent des détails morphologiques reliés à l’ensemble de cet « organisme » qu’est l’image en restructuration continue ; mais ces détails offrent également l’aspect de rup­tures, de discontinuités associées à des transitions, elles-mêmes fonction de l’échelle d’observation. De l’ensemble apparent du corps humain aux ultimes composants cellulaires, en passant par les fibres intermédiaires de la matière vivante, toutes les échelles d’exploration offrent de nouveaux spectacles de la nature humaine. Il en est de même pour les images fractales : les zoom en cascade, qui n’équivalent absolument pas à de simples agrandissements photographiques homothétiques puisqu’il faut recalculer inté­gralement l’image, engendrent d’étranges figures éternellement « intermédiaires ». En effet, tantôt l’on visualise des figures connexes, tantôt émer­gent de cette connexité des figures en poussière de points, ou encore des configurations incertaines, à la fois connexes et discontinues. La « loupe fractale » devient, selon l’expression de James Gleick dans son ouvrage La Théorie du Chaos, « un moyen de voir l’infini » (James Gleick, La Théorie du Chaos, éditions Albin Michel, Paris, 1989, p. 132).

Les créateurs de Fractales ont attribué des noms poétiques à ces figu­res extrêmement complexes et curieuses, remplies de détails enchevêtrés à l’infini au gré des échelles progressives d’exploration. Ces noms sont évocateurs de formes naturelles, végétales, géologiques ou animales. Ils parlent de vrilles, de galaxies, de spirales vers l’infini des profondeurs abyssales, d’oursins, d’hippocampes (« la Vallée des hippocampes »...), de nains grotesques, de gnomes, de créatures fantastiques, de paons, de scep­tres, de végétation luxuriante, de montagnes enchantées et de vallées ima­ginaires, de tourbillons effrénés, infernaux, et de fleuves tortueux, de cyclo­nes et de mers de coraux, d’îles et d’oasis, de marée et d’anneaux de Saturne, etc.

L’infinité des différences chromatiques et formelles résulte donc en prio­rité des variations scalaires qui sont pour ainsi dire la clé méthodologique amplificatrice de la récursion fonctionnelle. La récursion équivaut à une sorte de croissance ou de développement biogénétique des formes, tandis que la variation scalaire équivaut à des paliers, des stades ou des étapes de ce développement biologique illimité. La comparaison morphogénéti­que est d’ailleurs fréquemment évoquée par les créateurs de Fractales, voyant dans la métaphore du développement morphogénétique un principe de compréhension culturelle du « phénomène-fractalité ». L’originalité mor­phologique des images en chaque fraction de seconde du calcul itératif est l’équivalent du processus de différenciation biologique des organismes vivants au cours de leur croissance. Elle signe en même temps l’unicité absolue dans l’histoire de la création des formes, de l’originalité individuelle irréductible. Jamais deux Fracta­les strictement identiques en deux moments distincts du temps de calcul itératif, ne peuvent émerger de « l’alchimie » algorithmique.

Le discours métaphorique sur la création autoréférentielle des Fracta­les s’inscrit simultanément dans le domaine du vocabulaire histologique (la structure « tissulaire » en continuelle transition fractale, comprise entre 0 et 3 inclus) et dans le domaine généti­que. À cet égard, il est révélateur de la puissance onirique de ces images en restructuration continue, que scientifiques et artistes évoquent conjoin­tement l’idée du « code génétique » en parlant du développement indéfini du programme itératif de l’ordinateur. Les ensembles de Mandelbrot et de Julia (les plus connus parmi les ensembles fractals) sont comparés par leurs auteurs (en premier lieu par Mandelbrot lui-même) à des sculptures en modification continuelle. Des sortes de corps humains ou animaux en état de transition permanente, en somme.

Un expérimentateur d’images fractales, aussi esthète et poète que Jef­frey Ventrella (de l’Université de Syracuse, USA), considérait vers la fin des années 1980 qu’il engen­drait des créatures étranges en trois dimensions et en série évolutive de sur­croît, qui forment une véritable zoomorphologie dans le plan complexe. L’itération dans le plan complexe de la formule quadratique de base: (z² + c) → z, formule dans laquelle les paramètres littéraux z et c représentent des expressions complexes habituelles (en algèbre des nombres complexes), du type z ou c = a + ib (où i² = −1), cisèle à loisir des anatomies complexes et infiniment riches, aux innombrables facettes. Les fonctions fractales, par définition autorécursives ou autoréfé­rentielles, représentent un « code génétique » semblable à celui recelé par une spirale de molécules d’ADN.

Ainsi s’exprimait Jef­frey Ventrella à ce sujet, à la fin des années 1980 : « En explorant les mécanismes intérieurs d’une fonction et en décou­vrant des changements intéressants, on a l’impression de démêler la spi­rale d’ADN. Ceci est pour moi une des possibilités de la « biogénétique abstraite » […] Peter Oppenheimer du New York Institute of Technology et d’autres, ont comparé l’art fractal à la création biologique. » (in revue d’infographie Tech Image, numéro 4, janvier 1989, Paris, p. 19-20).

Ce langage pourrait, de prime abord, faire penser qu’il ne s’agit que d’une rêverie d’artiste enthousiaste, ayant de fortes tendances pour les paro­les hyperboliques. Il était pourtant entièrement partagé par des mathémati­ciens aussi hautement spécialisés dans les mathématiques de la fractalité que sont, notamment, en France, Adrien Douady, et aux États-Unis, John Hubbard, les deux chercheurs travaillant d’ailleurs en étroite collaboration.

Dans la formule basique du polynôme complexe programmé itérative­ment (c’est-à-dire en boucle récursive), le nombre complexe c adjoint au nombre complexe z élevé au carré (z pouvant être un nombre réel sans autre partie imaginaire) est considéré alors comme la clé génétique du pro­gramme ! Les ensembles de Julia et de Mandelbrot sont indéfiniment restructurés dans leur « anatomie » fractale complexe, dynamique et multiscalaire. Le principe de variation numérique indéfiniment réitérée du para­mètre complexe c engendre une classification algorithmiquement démon­trée (donc expérimentale) des types de nombres complexes et de leurs pro­priétés géométriques. Par le moyen d’un tel programme variatif, les for­mes les plus complexes se révèlent successivement selon l’imprévisibilité temporelle de leurs composantes morphologiques. Il s’agit d’un véritable développement d’information génétique selon Adrien Douady, qui écrivit alors dans une revue scientifique :

« Pour chaque valeur de c, le processus itératif défini par l’opération très simple (z²+ c) → z finit par sculpter l’ensemble de Julia, par lui donner sa forme compliquée, structurée et variée, suivant les valeurs de c. Ce faisant, il développe l’information contenue dans la clé c un peu comme l’ontogenèse d’un être vivant (développement de l’individu) déve­loppe l’information contenue dans l’ADN des chromosomes de l’œuf. » (Adrien Douady, in Images des Mathématiques - Le Courrier du CNRS, Supplément au numéro 62, Paris, 1985, p. 29-30).

Le thème chromosomique ne saurait s’affirmer dans un esprit d’analo­gie plus suggestif, et il est vrai que le déroulement du programme « épuise » à l’infini (mais n’épuise jamais exhaustivement en fait) les potentialités mor­phologiques du « germe c ». En théorie scientifique de l’information, on dit que le système dynamique va d’un ordre moindre à un ordre supérieur qui se dessine peu à peu en perdant de l’entropie (absence d'ordre relative, du point de vue statistique). Dans le cas des images fractales, au départ de la mise en oeuvre du programme, le « désordre » ou l’incertitude a priori concernant l’émer­gence morphologique sont au maximum, l’entropie est donc très forte. Puis, au fur et à mesure que s’exécute le programme récursif, l’image se complexifie dans toute sa précision et sa subtilité chromatique, avec tous ses détails imbriqués à l’infini (potentiellement tout au moins). ­

L’entropie diminue, mais elle ne saurait devenir nulle, au contraire, puisque la restructuration ico­nique est permanente et sans fin ; cependant, la nouveauté est aussi par­tiellement (pixel après pixel) et progressivement émergente : elle conserve l’information en même temps qu’elle la modifie, l’enrichit, lui apporte d'infinies nuances.

La comparaison entre programme fractal et programme génétique était affirmée encore plus directement par le mathématicien John Hubbard. En effet, la simplicité des deux types de programmes est sans doute leur caractéristique com­mune majeure. Un programme itératif de Fractales s’écrit très brièvement en quelques lignes d’instructions, mais l’énormité quantitative des calculs en chaîne, afin de détailler à l’infini une belle image aux nuances chro­matiques enchanteresses, est de taille ! À partir d’un petit programme de calcul, mais des temps plus ou moins importants de calcul portant sur des échelles variées d’exploration, une quantité illimitée de formes émerge de cette matrice géné­tique idéale qu’est le programme. Car le programme représente bien une sorte d’idéalité formatrice et informatrice (au sens de la théorie scientifi­que de l’information).

Comparativement, un programme génétique, envisagé sur la base de la séquence finie des gènes chromosomiques de l’ADN, est également rela­tivement simple et court (environ 200 millions de bits significatifs) ; mais le « recopiage » et la recombinaison de ces informations biologiques élémentaires, plu­sieurs centaines de milliards de fois, au cours des générations suc­cessives, ont conduit à des variétés morphologiques extrêmes et en nom­bre inouï. Le semblable (mais non la stricte identité intersubstitua­ble !) est souvent la règle, bien que la différence absolue et irréductible soit, quant à elle, la loi universelle de la transformation morphogénéti­que. Même les jumeaux homozygotes possèdent des différences, psycho­logiques aussi bien qu’anatomiques. L’analogie à travers l’altérité fonda­mentale règle la vie.

John Hubbard voyait alors, dans la contrainte formelle d’un programme biologique relativement court, disproportionné par rapport aux  très nombreuses opérations de recombinaisons qu’il permet, se profiler une sorte de loi du semblable biologique ayant son équivalent dans la brièveté du programme informatique des Fractales. Il déclare en effet à ce propos  que « Les deux phénomènes ont en commun des programmes de taille beau­coup plus petite que la diversité de leurs réalisations » et qu’il « semble incroyable que la faible information contenue dans l’ADN soit suffisante pour déterminer les formes biologiques compliquées des êtres vivants », à l’instar des Fractales dont les dessins sont parfois spécifiés par des programmes de  quelques lignes seulement (John Hubbard, in Pour la Science, numéro 153, juillet 1990, p. 8).

Une Fractale devient, selon ce type de discours, un modèle rationnel autant qu’esthétique de la transmission du génome humain et ani­mal. L’idée est séduisante, et son pouvoir de séduction imaginaire vaut bien, sans doute, qu’elle nous masque les irréductibles hétérogénéités exis­tant entre le champ de la connaissance biologique et celui de la théorie mathématique. Quant aux résultats proprement esthétiques concernant les images fractales numériques, ils n’ont aucune commune mesure avec la biologie ou les mathématiques qui sont pour­tant, ici, fondatrices.

2. Esthétique du transitoire

Les Fractales visualisées après arrêt sur le processus dynamique dont elles résultent ne sont en fait que des sortes d’instantanés photographiques. Ce sont des coupes arbitraires, tandis que le codage informatique des points d’image n’a en théorie aucune fin ; il est virtuellement infini et en devenir permanent. C’est par conséquent la vidéographie qui en offre la meilleure présentation possible, compte tenu, évidemment, de l’inévitable limitation matérielle de la résolution de l’écran électronique, rendant impossible (à toute échelle) l’exploration exhaustive de tous les points numériques du plan (le mot  « tous » renvoyant, en fait, à l’idée d’une infinité mathématique potentielle).

Ces instantanés électroniques ne doivent cependant en rien cacher l’aspect irrémédiablement transitoire de l’image fractale. Celle-ci est faite, dès sa programmation, pour émerger et se transformer en permanence, dans un remodelage sculptural simultané de toutes les micro-zones du plan auquel elle appartient, tout en conservant l’information originaire créée depuis la mise en fonctionnement du programme.

La transition est inscrite au coeur même de l’image fractale, puisque celle-ci procède, précisément, d’une loi algébrique de transformation récur­sive des trajectoires de points. Or, images du chaos et de certains types d’attracteurs étranges (apériodiques), les Fractales symbolisent avant tout, dans leur usage artistique, une nouvelle esthétique du transitoire, du remo­delage continuel. Un programme de création de Fractales fonctionne comme un système dynamique ouvert dont la mémoire est formée de strates coexis­tantes mais progressivement recouvertes les unes par les autres, de telle sorte que la richesse de l’information visuelle, à l’intérieur du cadre d’une même échelle ou par passage d’une échelle à une autre, résulte autant des conditions initiales de la mémoire informatique que de sa transformation continue.

Le système dynamique fractaliseur (loi fonctionnelle algébri­que + instructions programmées + trajectoires et codage chromatique des points dans le plan complexe, à une échelle d’exploration donnée) joue à la manière d’un système physique qui oublie progressivement les con­ditions initiales ou les états primitifs qui lui ont donné naissance. C’est pourquoi, à toute échelle, il y a émergence et enrichissement de l’infor­mation.

Le transitoire apporte ici de l’information nouvelle en permanence. Un système fractal se comporte un peu à la manière d’un système physique turbulent ou chaotique, dans la mesure où deux conditions initiales très voisines peuvent provoquer des résultats extrêmement différents. Ainsi, deux « germes numériques » complexes c, dans la formule récursive de base, aussi peu différents numériquement que l’on voudra, seront susceptibles de développer (de « créer ») des informations morphologiques en couleurs extrêmement variables, imprévisibles et différentes. Les physiciens du chaos parlent à ce propos de la propriété de sensibilité aux conditions initiales (écriture abrégée : SCI).

Les Fractales signifient, incontestablement, une esthétique mais aussi plus largement, une philosophie du transitoire, caractéristique des méthodes d’approche intellectuelle des sciences physiques, mathématiques et humai­nes du dernier quart du vingtième siècle. À ce titre, elles sont non seulement un phénomène techno-artistique dépendant de la technologie de l’information et de la science des modèles dynamiques, mais également un phénomène culturel révélateur d’une époque en mutation continue.

© Jean-Claude Chirollet