Fractals et Cartographie
1. Modèle cartographique et échelles descriptives
Pratiquement toutes les sortes de formes naturelles peuvent être considérées comme infiniment irrégulières et discontinues, en fonction des multiples échelles d'examen auxquelles on les soumet. Les exemples d'objets fractals puisés dans l'environnement naturel sont quasi omniprésents, et les sciences physiques et bilogiques découvrent qu'ils sont en extension continuelle. Ainsi, la structure métamorphique des nuages, les reliefs montagnards, le mappage omnidirectionnel d'un ciel étoilé, l'univers insondable des galaxies, tout comme une simple feuille de châtaignier, un morceau de rocher, un fragment de métal ou une cellule biologique, humaine, animale ou végétale, sont porteurs d'innombrables zones d'irrégularité morphologique en fonction des niveaux d'observation auxquels on les décrit. Le mérite scientifique (et poétique) de la géométrie fractale, c'est précisément d'avoir donné de puissants instruments mathématiques pour caractériser ces degrés ou niveaux d'irrégularité relative, qui signent l'hétérogénéité morphostructurale de la matière et de l'Univers tout entier.
Ce sont les échelles d'examen de l'objet, naturel ou purement géométrique, qui définissent les degrés variables de discontinuité morphologique, et l'intrication du continu et du discontinu au sein des formes de la nature. Le thème, bien connu en physique théorique, de l'interrelation opératoire de l'observateur avec l'objet observé, s'affirme en ce domaine mathématique comme le motif primordial de la détermination de la dimension fractale. Les objets de la nature, observés à grande distance – la notion de distance est elle-même relative à la taille de l'objert observé –, peuvent apparaître globalement comme des formes simples, bien régulières et continues, descriptibles au moyen des catégories de la traditionnelle géométrie euclidienne : des cercles, des triangles, des parallélépipèdes, des sphères, des cônes, des cylindres, des polyèdres, et toute combinaison de ces formes élémentaires primitives dont la pensée grecque antique avait alimenté ses spéculations, aussi bien mathématiques que métaphysiques.
Pourtant, observées de plus près, éventuellement au moyen de loupes et de microscopes, ces formes naturelles apparaissent beaucoup plus compliquées, moins linéaires, en un mot : moins « euclidiennes ». Elles présentent des contours brisés et des structures surfaciques ramifiées, enchevêtrées. Si le niveau d'observation, toujours plus exigeant, continue de s'affiner par l'intermédiaire de la loupe et du microscope, le moindre détail peut alors apparaître comme lui-même constitué d'une myriade de détails plus fins et toujours plus riches de microformes, elles-mêmes saturées à l'infini de microformes gigognes hyperdétaillées aux apparences nouvelles et imprévisibles.
Le corollaire de l'affinement de l'échelle d'observation réside dans le fait qu'aucune symétrie euclidienne connue n'est détectable en chaque fragment étudié. Les multiples niveaux mésoscopiques de la description, virtuellement infinis, ne semblent plus pouvoir être mis en corrélation hiérarchique continue, de même que les lois de la symétrie qui caractérisent généralement un objet dans sa totalité ne semblent plus pouvoir se révéler à travers les parcellisations de l'ensemble primitif. Il en résulte que tout fragment se manifeste comme une nouvelle totalité, étrangère morphographiquement, en apparence, à l'ensemble dont il est extrait comme un « détail » insituable. La loi d'unité et de concordance morphologique entre le tout et ses parties (la symétrie au sens étymologique grec) devient alors caduque, par l'application systématique, en chaîne, du jeu des variations d'échelles d'examen.
2. Cartographie multiscalaire d'un littoral
 Un modèle typique de raisonnement fractaliste, exposé par Benoît Mandelbrot dès 1967, est celui relatif à la mesure cartographique d'un littoral. La quantité et la précision descriptive des détails côtiers d'un littoral, tel que celui de la côte de Bretagne, sont fonction de l'échelle numérique de représentation adoptée par le cartographe. Ainsi, imaginons que l'on se propose de mesurer la longueur de la côte entre deux points géographiques donnés, au moyen d'un compas (fictif) d'écartement variable. Plus l'écartement sera important, plus la longueur obtenue sera de médiocre précision, et la carte qui correspondra à cette mesure sera très schématique, donc plus ou moins déformante. Il s'agit là de la technique dite de « généralisation » cartographique. Inversement, de très petits écartements produiront une mesure plus véridique, correspondant à une carte elle aussi nettement plus élaborée quant à ses détails. Mais la longueur obtenue par ce moyen toujours plus exigeant (des écartements de compas de plus en plus faibles), tendra vers une grandeur infinie, car il s'agira dans cette éventualité de prendre en compte les moindres anfractuosités du rivage, des rochers en particulier. [↑ Image ci-dessus : Littoral dentelé de la côte bretonne, figuré selon une petite échelle de grandeur. La limite entre terre et mer est fluctuante, difficilement traçable car extrêmement irrégulière.]
Un modèle typique de raisonnement fractaliste, exposé par Benoît Mandelbrot dès 1967, est celui relatif à la mesure cartographique d'un littoral. La quantité et la précision descriptive des détails côtiers d'un littoral, tel que celui de la côte de Bretagne, sont fonction de l'échelle numérique de représentation adoptée par le cartographe. Ainsi, imaginons que l'on se propose de mesurer la longueur de la côte entre deux points géographiques donnés, au moyen d'un compas (fictif) d'écartement variable. Plus l'écartement sera important, plus la longueur obtenue sera de médiocre précision, et la carte qui correspondra à cette mesure sera très schématique, donc plus ou moins déformante. Il s'agit là de la technique dite de « généralisation » cartographique. Inversement, de très petits écartements produiront une mesure plus véridique, correspondant à une carte elle aussi nettement plus élaborée quant à ses détails. Mais la longueur obtenue par ce moyen toujours plus exigeant (des écartements de compas de plus en plus faibles), tendra vers une grandeur infinie, car il s'agira dans cette éventualité de prendre en compte les moindres anfractuosités du rivage, des rochers en particulier. [↑ Image ci-dessus : Littoral dentelé de la côte bretonne, figuré selon une petite échelle de grandeur. La limite entre terre et mer est fluctuante, difficilement traçable car extrêmement irrégulière.]
C'est le principe même du zoom numérique, opéré en cascade sur les structures fractales autosimilaires (hyperfractals), obtenues par l'application d'algorithmes récursifs (renormalisation géométrique). L'aspect morphologique infiniment sinueux et granuleux de la moindre parcelle microscopique de matière pourrait, en théorie, être apprécié par des instruments d'observation métrologique ultraprécis, détectant des longueurs microscopiques de l'ordre d'une fraction d'angström par exemple (l’angström vaut un dix-millionième de millimètre), et la longueur du littoral s'accroîtrait alors 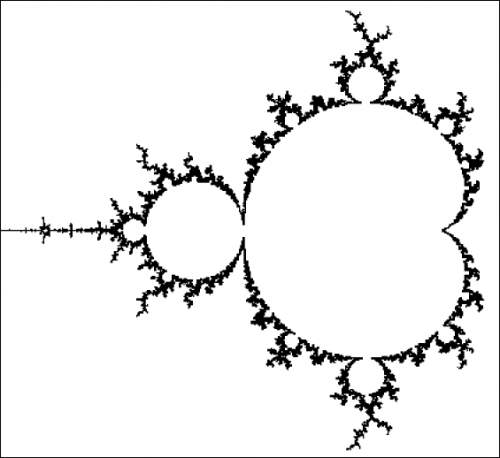 indéfiniment. Mais la carte
indéfiniment. Mais la carte
physiquement réalisable ne pourrait plus réellement prendre en compte cette extrême profusion de détails. D'ailleurs, les conventions cartographiques habituelles limitent la représentabilité du territoire, bien avant d'atteindre cette luxuriance morphographique fictive à l'échelle de l'angström ! [→ Image ci-contre : Vue générale de la frontière de l'ensemble autosimilaire de Mandelbrot, infiniment dentelée et irrégulière, comparable à la pseudo-limite fluctuante de la côte bretonne.]
La longueur de la côte tendant vers l’infini en raison de son extrême irrégularité physique, et en fonction de l’échelle d’examen de plus en plus fine (résolution métrologique), sa dimension fractale D n’est pas égale à la dimension topologique entière d’une ligne continue (idéale) de la géométrie euclidienne (D = 1), mais à une dimension non-entière, fractionnaire, comprise entre D = 1 (la ligne idéalement continue) et D = 2 (une surface plane), assez proche cependant de la dimension topologique d’une ligne continue (D = environ 1,16 à 1,2 en fonction de la précision des instruments de mesure théoriques utilisés). [Cf. Benoît Mandelbrot, Les Objets fractals – Forme, hasard et dimension, Chapitre II (Combien mesure donc la côte de Bretagne ?), 4è éd. revue, Paris, Flammarion, 1995.]
Cet exemple de représentation cartographique d'un littoral, qui conduit jusqu'aux confins de la pure imagination, est révélateur de l'importance primordiale de l'échelle d'observation des phénomènes. Il fait comprendre la spécificité de la notion d'objet fractal : un objet fractal est en fait un objet mathématique, même si au départ la réflexion porte sur des objets réels (naturels ou artificiels), car la dimension abstraite (ou indice) fractionnaire qui le caractérise est le résultat objectif d'un raisonnement algébrique, qui met en jeu l'itération ad infinitum d'un calcul de grandeurs, référées à  une succession d'échelles métrologiques : depuis les rapports d’échelle de réduction [1 : X], jusqu'aux rapports d’échelle d’agrandissement [X : 1], avec X > 1, en passant par l'échelle grandeur nature [1 : 1] (avec X = 1).
une succession d'échelles métrologiques : depuis les rapports d’échelle de réduction [1 : X], jusqu'aux rapports d’échelle d’agrandissement [X : 1], avec X > 1, en passant par l'échelle grandeur nature [1 : 1] (avec X = 1).
Or, toute cartographie demeure indéfiniment approchée, puisqu'elle est liée à l'adoption concomitante d'un système formel codifié, et d'une échelle relative de représentation, dont la résolution est spécifiquement adaptée au système. Les conventions cartographiques de la représentation d'un pays entier au ratio [1 : 1 000 000] ne sont pas celles relatives à la représentation d'un plan de ville ou de quartier au ratio [1 : 10 000]. De même, les méthodes photomicrographiques appliquées à un fragment de cellule humaine ou végétale, qui multiplient la taille réelle de l'objet, invisible à l'œil nu, par un coefficient d'agrandissement de l'ordre de 50 000 fois à 250 000 fois, apportent leurs règles technologiques spécifiques de représentation.
3. Relativité d'échelle et résolution métrologique
Le réel appréhendé sélectivement en fonction d'une certaine échelle de grandeur, c’est-à-dire selon un niveau particulier de révélation des détails, entraîne de facto le renoncement (tout au moins provisoire) à percevoir ce qui existe à une échelle  supérieure ou inférieure. Ainsi, la prise de distance excessive, par l’utilisation instrumentée d’une très petite échelle de représentation cartographique (très généralisante), exclut la saisie des détails significatifs d’un phénomène, au profit exclusif de la compréhension d’ensemble. Inversement, si l’attention est immergée dans la complexité des plus infimes détails et particularités, par l’intermédiaire d’une échelle d’observation hyperfine, elle devient alors incapable de saisir l’ensemble d’où ils sont extraits. Il en découle donc logiquement que l’impuissance d’une échelle d’examen, trop fine ou bien, inversement, trop extensive, relativement à un niveau de description ou d’explication du réel, peut constituer, en sens inverse, sa force et sa pertinence à l’égard d’un niveau descriptif ou explicatif différent.
supérieure ou inférieure. Ainsi, la prise de distance excessive, par l’utilisation instrumentée d’une très petite échelle de représentation cartographique (très généralisante), exclut la saisie des détails significatifs d’un phénomène, au profit exclusif de la compréhension d’ensemble. Inversement, si l’attention est immergée dans la complexité des plus infimes détails et particularités, par l’intermédiaire d’une échelle d’observation hyperfine, elle devient alors incapable de saisir l’ensemble d’où ils sont extraits. Il en découle donc logiquement que l’impuissance d’une échelle d’examen, trop fine ou bien, inversement, trop extensive, relativement à un niveau de description ou d’explication du réel, peut constituer, en sens inverse, sa force et sa pertinence à l’égard d’un niveau descriptif ou explicatif différent.
Il n’existe pas, en réalité, d’échelle absolue ou exhaustive d’examen ou de vision, mais seulement et irrémédiablement des échelles sélectives, mieux adaptées que d’autres, définies d'une part en fonction d’une intention du regard instrumenté, et d'autre part de la volonté de comprendre ou de décrire certains aspects particuliers des choses qui nous entourent, au moyen de représentations ad hoc : figures géométriques, graphiques et schémas, plans et cartographies, descriptions, concepts (en sciences et philosophie). Prétendre définir une échelle d’observation soi-disant « absolue » pour décrire un phénomène, n’aurait aucun sens : seuls les rapports comparatifs entre échelles différentes possèdent une signification afin de décrire les phénomènes de la nature, tout autant que les artefacts humains. Des réalités insoupçonnées à une certaine échelle de représentation, se révèlent de manière significative à une échelle supérieure de résolution numérique, mieux adaptée au niveau de réalité dont le cartographe veut donner l’image. De même, dans le domaine de la géométrie fractale, les rapports d’échelles sont directement associés aux résolutions spatiales comparées, utilisées pour la description des formes physiques ou mathématiques.
 Appliqué à la physique de la Nature et à la cosmologie, le concept de « rapports d’échelles », fonction de la résolution métrologique des systèmes de référence utilisés, est devenu essentiel pour comprendre la structure fractale de l’Univers. Évoquons à cet égard, notamment, les travaux du physicien français Laurent Nottale, menés à partir des années 1990, qui a développé ce thème scientifique sous le terme de « relativité d’échelle » (ou relativité fractale), en attribuant au concept de résolution métrologique le rôle de variable essentielle de l’espace-temps fractal. [Cf. Laurent Nottale, La Relativité dans tous ses états – Au-delà de l’espace-temps, éd. Hachette Littératures, Paris, 1998.]
Appliqué à la physique de la Nature et à la cosmologie, le concept de « rapports d’échelles », fonction de la résolution métrologique des systèmes de référence utilisés, est devenu essentiel pour comprendre la structure fractale de l’Univers. Évoquons à cet égard, notamment, les travaux du physicien français Laurent Nottale, menés à partir des années 1990, qui a développé ce thème scientifique sous le terme de « relativité d’échelle » (ou relativité fractale), en attribuant au concept de résolution métrologique le rôle de variable essentielle de l’espace-temps fractal. [Cf. Laurent Nottale, La Relativité dans tous ses états – Au-delà de l’espace-temps, éd. Hachette Littératures, Paris, 1998.]
En premier lieu, ce qu'enseignent ces méthodes variées de représentation multiscalaire, c'est la nature intrinsèquement mésoscopique de toute image du réel : le « microscopique », quel que soit son niveau d'appréhension, n'est toujours qu'un intermédiaire, un relais entre des mondes infiniment plus petits que lui, et des mondes infiniment plus grands. Il en est de même pour le « macroscopique », dont les dimensions appréhensibles sont infiniment grandes pour les niveaux très inférieurs à lui, mais qui se réduit à un niveau en quelque sorte microscopique, en référence à des niveaux scalaires très supérieurs au sein de l'immensité de l'Univers.
En second lieu, on peut affirmer logiquement que les conventions graphiques et géométriques sous-tendant les représentations cartographiques, constituent un  système formel susceptible de décrire non seulement toute la réalité géographique visible, à une échelle adaptable aux formats de la représentation globale sur le papier (territoires entiers), mais aussi à toute échelle théorique fixée arbitrairement, aussi grande soit-elle (plans détaillés, détails matériels, etc.). L'échelle et les modes de représentation, certes, devront changer à chaque étape : des représentations macroscopiques jusqu'aux représentations microscopiques du réel, mais en théorie le principe d’agrandissement ou de réduction scalaire peut s'appliquer en cascade ad libitum, par le jeu opératoire des échelles mésoscopiques successives.
système formel susceptible de décrire non seulement toute la réalité géographique visible, à une échelle adaptable aux formats de la représentation globale sur le papier (territoires entiers), mais aussi à toute échelle théorique fixée arbitrairement, aussi grande soit-elle (plans détaillés, détails matériels, etc.). L'échelle et les modes de représentation, certes, devront changer à chaque étape : des représentations macroscopiques jusqu'aux représentations microscopiques du réel, mais en théorie le principe d’agrandissement ou de réduction scalaire peut s'appliquer en cascade ad libitum, par le jeu opératoire des échelles mésoscopiques successives.
→ Les 4 photographies de paysages ci-dessus : 4 vues de détail de la Pointe-du-Raz (côte de Bretagne), correspondant à différentes échelles de représentation. Passer d'une représentation cartographique, quelle qu'en soit l'échelle, au territoire concret, c'est entrer dans une infinité de détails matériels gigognes, invisibles aux échelles de représentation cartographique habituelles, à la manière des détails d'une image fractale autosimilaire. Cependant, en pratique, une carte géographique doit s'arrêter aux formes paysagesques macroscopiques, dont la représentation est utile pour le repérage in situ.
[Cf. aussi l'article → Théâtre et Chaos fractal / "Arcadia" de Tom Stoppard (1993) Partie II]
© Jean-Claude Chirollet
