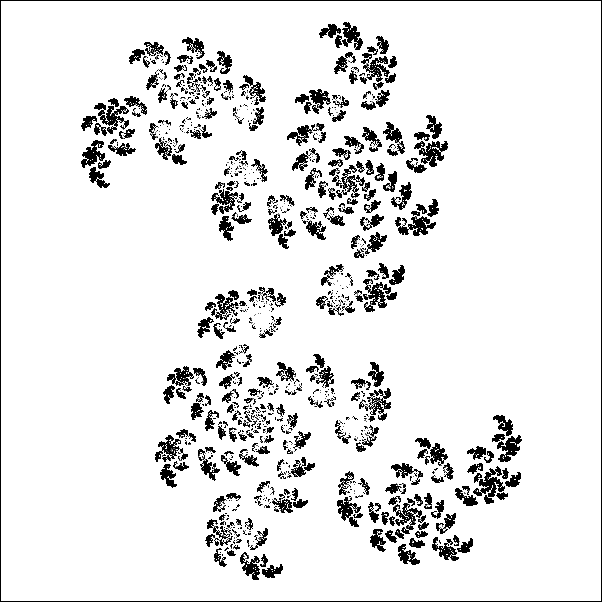Arts / Numérisation / Fractals

 1. Ensemble de Mandelbrot et Ensembles de Julia : Schémas-types

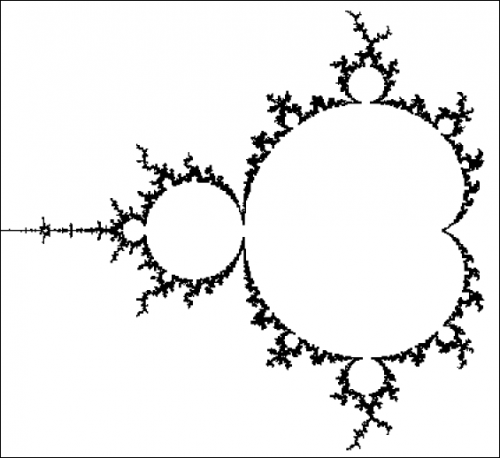
Figure 1. Vue générale, à petite échelle, de la frontière de l'ensemble de Mandelbrot.

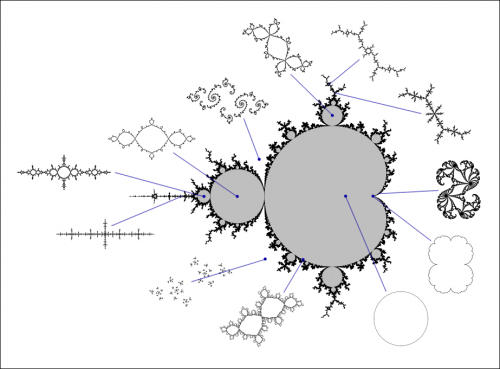
Figure 2 (ci-contre →) et Figure 3 (ci-dessous ↓). Vues schématiques de différents types d'ensembles de Julia (il y en a une infinité), associés à l'ensemble de Mandelbrot, obtenus par zooms numériques sur des points de la frontière ou de l'intérieur de l'ensemble de Mandelbrot.

Figure 4. Vue schématique en noir-et-blanc d'un type d'ensemble de Julia connexe, obtenu par l'agrandissement digital d'un mini-détail de la frontière de l'ensemble de Mandelbrot. 

 Figure 5. Vue schématique en noir-et-blanc d'un type d'ensemble de Julia non-connexe, obtenu par l'agrandissement digital d'un mini-détail de la frontière de l'ensemble de Mandelbrot.

 2. Fonctions quadratiques récursives dans le plan complexe

2.1 – Sans entrer ici dans la théorie algébrique proprement dite des fonctions polynomiales (qui n'est pas le but de cet article), il faut savoir simplement, tout d'abord, que les fonctions mathématiques à partir desquelles sont engendrées les figures fractales ci-dessus : l'ensemble de Mandelbrot et les ensembles de Julia, sont des fonctions polynomiales quadratiques ou « fonctions polynômes » de degré d = 2, du type : f(x) = ax + bx² + c où a, b et c désignent des constantes réelles, a et b étant des coefficients entiers positifs ou négatifs, et c pouvant être éventuellement nul. Par exemple : y = f(x) = 4x + 3x² + 1. Une fonction polynomiale peut être de degré entier 2, 3, 4, ... quelconque. Les fonctions quadratiques sont par conséquent les fonctions polynômes les plus simples. Les fonctions de degré d = 1, du type : y = f(x) = ax + b où a et b désignent des constantes réelles quelconques, par exemple : y = f(x) = 5x + 3, sont des fonctions dites « affines ». Leur comportement algébrico-géométrique est évidemment plus simple et prédictible que celui des fonctions polynomiales de degré d ≥ 2, mais dans le deux cas il s'agit de fonctions linéaires.

2.2 – Or, la particularité fondamentale des fonctions quadratiques permettant d'obtenir le tracé des ensembles de Mandelbrot et de Julia, c'est d'une part qu'elles intègrent dans leur calcul des paramètres complexes de la forme c = a + ib (où i² = −1), et que d'autre part ce sont des fonctions récursives, c'est-à-dire dont le calcul des valeurs successives de la fonction dans le plan complexe s'auto-alimente, à chaque étape t du calcul en chaîne, du résultat obtenu à l'étape précédente t – 1. Une fonction récursive fait donc, pour ainsi dire, « appel à elle-même » dans le processus de calcul de ses valeurs successives. Pour cette raison, il s'agit de fonctions polynomiales non-linéaires, dont le comportement plus ou moins rapidement imprédictible à moyen ou long terme, simule au bout d'un certain nombre d'étapes le comportement chaotique d'un attracteur étrange.

Le processus algorithmique de calcul en série porte donc sur un paramètre complexe initial fixe : c = Z₀ = (a + ib), a et b réels – par exemple : Z₀ = 0,1 + 0,02i ou Z₀ = 0,05 (avec b = 0) – qui fait office d'état initial du système dynamique. Puis s'enchaînent en cascade les itérations suivantes, avec f_c(Z) = Z² + c (fonction quadratique récursive) :

 Z₁ = f(Z₀) → Z₂ = f(Z₁) → Z₃ = f(Z₂) → Z₄ = f(Z₃) → Z₅ = f(Z₄) → (...) → Z_n = f(Z_n-1)... etc.

La suite des nombres Z_n calculés itérativement, crée un ensemble de points potentiellement infiniment dense en certaines zones du plan complexe, en « ciselant » progressivement, d'après des règles fonctionnelles définies rigoureusement (exposées dans les paragraphes suivants), les ensembles fractals de Mandelbrot et de Julia.

2.3 – Soit un nombre complexe de départ c = Z₀ (c = a + ib), puis la suite des itérations construite à partir de ce nombre complexe :  Z₁ = f(Z₀) → Z₂ = f(Z₁) → Z₃ = f(Z₂) → Z₄ = f(Z₃) → Z₅ = f(Z₄) → (...) → Z_n = f(Z_n-1)... etc., où f_c(Z) = Z² + c. L'ensemble J_c des nombres Z₀ dont la suite des itérés ne s'éloigne pas indéfiniment du centre du plan complexe (c'est-à-dire : dont le module en valeur absolue ne tend pas vers l'infini), définit « l'ensemble de Julia rempli », selon le vocable des mathématiciens. Un ensemble de Julia est donc l'ensemble des nombres complexes Z₀ dont la suite des itérés reste bornée. La frontière de l'ensemble J_c est dénommée simplement « ensemble de Julia ». Un ensemble de Julia – il en existe d'infinies variétés en fonction de c = Z₀ – décrit par conséquent la dynamique des trajectoires de points qui est celle de la variable Z, puisque la fonction quadratique récursive de base fonctionne comme un système dynamique autoréférentiel.

Les configurations morphologiques adoptées par l'ensemble de Julia rempli J_c sont 

extrêmement diverses, selon la valeur de la variable complexe c sélectionnée. En particulier, les ensembles de Julia peuvent être soit connexes (constitués d'un seul tenant, en un seul « morceau »), soit non connexes : dans ce cas, ils sont éparpillés, pulvérisés à la manière d'une « poussière de Cantor » (ensemble triadique de Cantor). Si J_c est connexe, et s'il possède un intérieur, celui-ci peut éventuellement ne pas être connexe, mais formé d'un ensemble infini de composantes fractales dissociées ; le langage mathématique parle, dans ce cas-là, d'un ensemble de Julia « pincé ». [↑ Cf. Figures 2, 3, 4 et 5 ci-dessus.]

2.4 – Les ensembles de Julia sont géométriquement associés à l'ensemble de Mandelbrot, cette expression désignant l'ensemble M des paramètres complexes c (c = a + ib), tels que les ensembles de Julia J_c soient connexes. On peut aussi en donner cette définition algébrique équivalente : l'ensemble de Mandelbrot M est constitué de l'ensemble des points c du plan complexe, pour lesquels la suite itérative (définie par récurrence) des points Z_n = (Z_n-1)² + c, avec Z₀ initial de valeur nulle (Z₀ = 0), ne tend pas vers l'infini (c'est-à-dire : le module en valeur absolue des nombres complexes Z_n ne tend pas vers l'infini), mais reste située dans un disque fermé de rayon r fini (r = 2 ou r = 3 par exemple). L'ensemble-type M de Mandelbrot décrit, par conséquent, l'espace des paramètres c dans le plan complexe auquel il appartient, à la différence d'un ensemble de Julia J_c qui décrit la dynamique des trajectoires de points qui est celle de la variable Z (Cf. § 2.3 ci-dessus).

Les points de l'ensemble M et la collection, potentiellement infinie, des ensembles de Julia J_c, sont structurellement apparentés. Notamment, quand le paramètre complexe c est un point de M, il est également un point d'un ensemble de Julia rempli J_c. En outre, il existe une grande similitude, révélable par un zoom numérique réalisé selon une échelle 

d'agrandissement adéquate (variable selon les cas), entre une petite région située autour d'un point c dans M, et cette même mini-région dans l'ensemble de Julia J_c correspondant. Il faut que le zoom sur la mini-région de M et de J_c soit effectué avec un grossissement suffisamment important, et qu'il soit accompagné d'une simple rotation géométrique, pour que soit vérifiée une telle similitude morphologique.

On peut aussi engendrer des fractals de type Mandelbrot ou Julia, dérivés de l'ensemble-type M, en choisissant des valeurs de Z₀ non nulles (Z₀ ≠ 0). Il est également possible de changer de type de fonction polynomiale, en choisissant par exemple une fonction récursive de degré entier 3, 4 ou supérieur, voire en adoptant des degrés fractionnaires. Ces ensembles fractals « exotiques » (ensembles fractals généralisés de Julia et Mandelbrot) possèdent des morphologies très différentes, bien que parfois apparentées à celle de l'ensemble M de Mandelbrot défini pour Z₀ = 0, en raison de certaines de leurs propriétés géométriques dans le plan complexe. [Cf. site CNRS → Méthode de Newton et Fractals.]

Or, l'ensemble M contient de petites copies emboîtées et déformées de lui-même, donc des mini-copies gigognes similaires, mais légèrement différentes entre elles (elles ne sont pas strictement auto-identiques à toute échelle, comme dans le cas des fractals scalants). Un point de M localisé dans une mini-copie est renormalisable dans le plan complexe, c'est-à-dire qu'il est agrandissable (zoomable) en chaîne indéfiniment, ou bien seulement un nombre fini de fois, à diverses échelles supérieures de grandeur. Un théorème mathématique démontré par le mathématicien français Jean-Christophe Yoccoz (médaille Fields 1994), dit que l'ensemble M est localement connexe, c'est-à-dire d'un seul tenant (ce n'est pas une « poussière de points » cantorienne), sauf (sans doute) aux points infiniment renormalisables de M, lesquels sont extrêmement nombreux cependant.

De plus, la frontière de l'ensemble M possède une dimension fractale égale ou quasi-égale à 2, c'est-à-dire que sa complexité géométrique, déjà appréhensible intuitivement par le calcul récursif des points à d'innombrables échelles d'exploration, lui confère la dimension enveloppante d'une surface plane. Ce résultat, établi au début des années 1990 par le mathématicien japonais Mitsuhiro Shishikura, signifie que la frontière infiniment irrégulière de M remplit l'espace complexe presque comme une surface, bien que son aire soit nulle.

3. Zooms en cascade sur l'ensemble de Mandelbrot

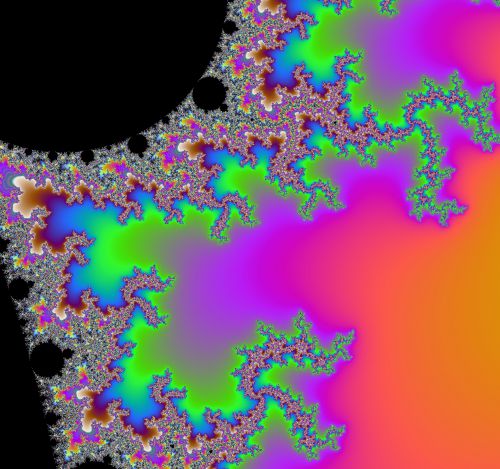
Les fractales numériques ci-dessous : Figure 1 → Vue générale à petite échelle – en quelque sorte « de loin » – de l'ensemble de Mandelbrot, suivie de 5 zooms numériques en cascade → Figures 2, 3, 4, 5 et 6, effectués à partir d'une zone autour de la frontière de cet ensemble, calculés en fonction d'un niveau de résolution choisi arbitrairement, une infinité de niveaux de résolution étant théoriquement possibles, seule la puissance de calcul de l'ordinateur étant limitée dans le temps, au bout d'un nombre plus ou moins grand d'itérations (par exemple : 50 000, 100 000, 1 000 000, etc.). La relation : résolution-définition, ainsi que la particularité morphologique locale des zones de dimension variable, sélectionnées pour effectuer les zooms numériques en cascade (algorithmes de renormalisation), conditionnent l'émergence de morphologies fractales autosimilaires, avec une intrication gigogne virtuellement « à l'infini » d'ordre et de désordre, de relative continuité morphologique (connexité) et de discontinuité ponctuelle. La palette plus ou moins riche des couleurs, définie arbitrairement, se répartit en fonction des règles du calcul récursif des points (itération mathématique), distribués dans le plan complexe.

  ← Figure 1

  Figure 2 →

 ← Figure 3  

  Figure 4 →

  ← Figure 5

 Figure 6 →

4. Compléments documentaires

a) L'article Ensemble de Mandelbrot de Wikipédia, outre les précisions mathématiques approfondies qu'il procure, met en scène la renormalisation géométrique de l'ensemble M au moyen d'illustrations numériques, fixes et animées, qui sont très démonstratives. On peut y voir, notamment, une série de zooms commentés, dans un très fort rapport de grossissement entre la dernière et la première image calculées, qui est d'environ 60 milliards (facteur de zoom d'environ 10³⁰). — Cf. aussi le lien ci-après : Vidéo sonore d'un zoom fractal ad infinitum : [→ Hologramme fractal].

b) Ci-joint un dossier PDF de synthèse très clair, sur les nombres complexes et les ensembles fractals de Julia et de Mandelbrot, écrit par Jean-Pierre Louvet sur le site Futura-Sciences.com :

  Ensembles fractals de Julia et de Mandelbrot 

© Jean-Claude Chirollet