Arts / Numérisation / Fractals

Les fractals géométriques semi-déterministes et les images fractales autosimilaires, obéissent très souvent à un comportement chaotique, typique des attracteurs étranges étudiés par les mathématiciens et les physiciens de la complexité informationnelle. Pour cette raison, il est utile de préciser le sens des termes employés dans ce registre de la technoscience des fractales et de la théorie du chaos (complexité).

1. Nombres Réels (R), Complexes (C), Hypercomplexes (H)

– Nombres réels : corps algébrique R qui comprend l’ensemble des nombres « ordinaires » utilisés par les mathématiciens et les physiciens : les entiers naturels N (0,1,2,3...) ; les nombres entiers relatifs Z (...-3, -2, -1, 0, +1, +2, +3, ...) ; les nombres fractionnaires ou « rationnels » Q (du type [a / b]) qui sont des rapports d’entiers ; les nombres irrationnels Q', irréductibles à des rapports d’entiers. Ces derniers possèdent une infinité de décimales non périodiques, par exemple le nombre π = 3,141 592 654... ou le célèbre Nombre d’Or des artistes classiques : φ = (1 + √5) / 2 = 1,618 033 989... Les nombres réels sont utilisés, notamment, dans le calcul des fonctions affines classiques. Ils sont symbolisés par une droite illimitée sur laquelle sont répartis les réels, positifs et négatifs, de manière entièrement ordonnée, de part et d'autre de la valeur zéro : de 0 à l'infini positif (+ ∞) et de 0 à l'infini négatif (− ∞).

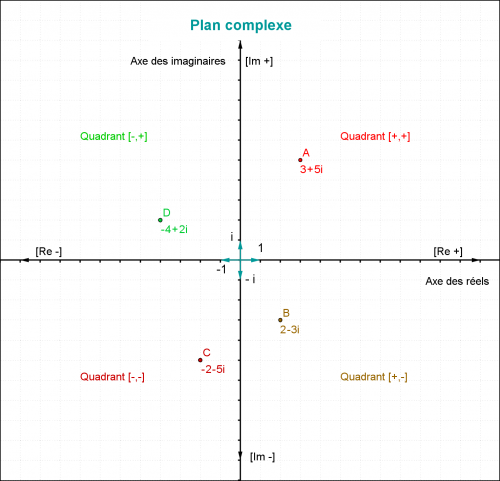– Nombres complexes : couple de nombres réels (a, b) traduits dans l’intégralité du plan complexe, du genre Y = a + ib où i² = −1, possédant leurs règles spécifiques de calcul algébrique. Exemple : Y = 5 + 7,5i. Les nombres complexes (formant le corps algébrique C) sont des extensions algébriques des nombres réels (corps R). Ils sont représentés dans l'intégralité de l'espace plan sur 360 degrés décimaux, comme des couples de réels (a,b) au sein d'un repère géométrique orthonormé. À ce titre, ils détiennent des propriétés algébriques différentes de ces derniers. Les fonctions récursives servant à calculer les fractales bidimensionnelles (comme l'Ensemble fractal de Mandelbrot en 2D), sont composées de nombres complexes C. Une figure fractale autosimilaire est un sous-ensemble du plan complexe, calculé récursivement (principe d'autoréférence) en fonction d'une certaine résolution numérique, choisie arbitrairement. [↑ Image ci-dessus : représentation du plan complexe (Cliquez !)]

Ci-joint (fichier pdf) certaines notions essentielles de trigonométrie, relatives aux propriétés algébriques du plan complexe et des nombres complexes.

Plan complexe et Trigonométrie.

– Nombres hypercomplexes : corps algébrique H de nombres qui étendent les propriétés des nombres complexes C. Les nombres hypercomplexes appelés « quaternions » (corps algébrique H), imaginés en 1843 par le mathématicien irlandais William Hamilton (1805-1865), sont des nombres à 4 composantes. Ils sont du type : q = a + ib + jc + kd, où a, b, c et d sont des nombres réels, et i² = j² = k² = ijk = −1 (nombres imaginaires).

 Le corps H des quaternions n'est pas commutatif. L'algèbre des quaternions permet notamment de décrire des rotations d'objets dans l'espace 3D, et de créer des images fractales représentées dans l'espace tridimensionnel. Les quaternions sont utilisés dans les équations polynomiales destinées au calcul des images fractales simulant le relief, avec des effets de perspective 3D. [→ L'image fractale ci-contre : Coupe en 3D des anfractuosités d'un détail de fractale de Mandelbrot en 3D – dite "Mandelbulb" –, créée à partir de quaternions H.] Signalons enfin que des algèbres encore plus extensives que celle des quaternions H, sont à l'origine de nombres hypercomplexes appelés « octonions » (nombres O à 8 composantes) et « sédénions » (nombres S à 16 composantes). Octonions et sédénions servent aussi parfois à créer des images fractales tridimensionnelles.

2. Renormalisation géométrique / Zoom numérique

Le calcul dans le plan complexe des points d’une image fractale peut s’effectuer, en théorie, à une infinité d’échelles possibles. Lorsque le calcul est arrêté à un certain stade de la programmation itérative (au bout de dix-mille étapes, par exemple), les détails pour cette échelle d'exploration peuvent alors être à nouveaux explorés à une échelle supérieure qui révèlera de nouveaux détails imprévisibles. Une parcelle de l’image « complète » de départ servira de terrain d’exploration, agrandie au même format (c'est-à-dire ici : avec une même définition numérique) que l’image intégrale dont elle est « extraite », par calcul à l’échelle supérieure : il s’agit d’une opération de renormalisation géométrique. À son tour, cette nouvelle image agrandie pourra devenir un terrain d’exploration pour de multiples autres agrandissements de micro-parcelles, au même format iconique mais à des échelles de calcul encore plus grandes, et ainsi de suite à l’infini. Les figures géométriques complexes formées par les images fractales, mêlent inextricablement le continu apparent (des quasi-lignes et des quasi-surfaces) et le discontinu (des simili-points, plus ou moins petits et denses). Des exemples typiques de l'opération de renormalisation géométrique, sont fournis par le fameux ensemble de Mandelbrot et les innombrables ensembles de Julia qui lui sont associés.

La mathématique des systèmes dynamiques parle de « groupe de renormalisation » pour désigner les techniques mathématiques permettant de calculer des figures fractales chaotiques (semi-déterministes), en fonction d'une infinité (potentielle) d’échelles successives. Un zoom numérique est engendré par renormalisation géométrique. On le définit comme un grossissement, dit aussi « effet-loupe », à une échelle d’agrandissement donnée, d’une image ou d’une portion d’image. Le zoom photographique par variation de focale est simplement homothétique, tandis que le zoom numérique (logiciel) effectué sur une partie d’image fractale semi-aléatoire, nécessite de recalculer intégralement cette portion iconique en révélant des détails morphologiques toujours nouveaux bien que globalement similaires (autosimilarité statistique). Il n’est donc pas homothétique mais agit par autosimilarité semi-déterministe (chaotique), les détails nouveaux qui émergent du processus de calcul itératif à une nouvelle échelle, par renormalisation, n'étant pas morphologiquement identiques à l’image d’ensemble antérieure dont ils proviennent.

Au contraire, un zoom photographique agrandit une partie d’image, mais tout en lui conservant exactement sa forme d’origine. Un zoom photographique permet certes d’entrer jusque dans le grain du film, dans sa structure moléculaire, mais l’information utile au sens strict, concernant la morphologie de l’image en elle-même, n’augmente pas, contrairement à l’information apportée par l’examen multiscalaire d’une image fractale semi-déterministe, statistiquement autosimilaire. Dans ce dernier cas, il existe une ressemblance morphologique générale entre l’ensemble et ses parcelles, mais chaque partie est en réalité différente de toute autre, éventuellement de manière seulement infinitésimale, à un « iota près ». Le micro-détail fait parfois toute la différence morphologique...

3. Equation polynomiale / Fonction non-linéaire (récursive) :

Une équation polynomiale est une fonction du genre Y = ax² + bx + c, comprenant deux ou plusieurs paramètres. Exemple : Y = 3x² + 4x + 3. Le degré de l’équation (ici degré 2) peut être quelconque (2, 3, ..., n). Une fonction non-linéaire est une fonction dont l’évolution géométrico-algébrique est imprévisible à court, moyen ou long terme, car régie par le principe d’autoréférence algébrique. Une fonction linéaire du type Y = (ax² + b) est parfaitement calculable à l’avance, en chacun de ses points infiniment denses (infini non-dénombrable) dans tout intervalle fermé de R (corps des nombres réels), et son tracé géométrique ne pose aucun problème. Par contre une fonction récursive, c'est-à-dire 

obéissant au principe d’autoréférence algébrique, du type Z ↔ (Z³ + iC), où Z et C désignent des nombres complexes du type [a + ib], devient très rapidement imprévisible. Elle est pourtant simple en soi, et son algorithme programmable s’énonce en quelques lignes d’instructions. Qu’en serait-il alors de fonctions beaucoup plus complexes comprenant de multiples paramètres ainsi qu’un principe de calcul aléatoire (calcul « randomisé »)...

4. Autoréférence / Boucle récursive

Principe par lequel un système (physique, mathématique, biologique) évolue en « se nourrissant de lui-même », c’est-à-dire en réintégrant continûment dans son comportement spatio-temporel, le résultat de ses expériences antérieures. Le principe d’autoréférence s’applique, en particulier, au comportement des équations polynomiales en « boucle récursive », utilisées notamment dans la programmation des fractals géométriques et des images fractales. On appelle « boucle récursive » le système de calcul des valeurs numériques d’une équation polynomiale (ou d’un système d’équations) du second ou du énième degré, par lequel à chaque étape de calcul, le résultat obtenu à la dernière étape est immédiatement réinjecté dans le processus de calcul à titre de nouvelle valeur paramétrique, pour obtenir la valeur suivante. — La récursivité renvoie donc au processus d'autoréférence, mais s'applique à l’algèbre des fonctions polynomiales. Une fonction récursive se calcule par itération indéfinie du même algorithme de calcul, en réinjectant systématiquement « en boucle circulaire », chaque valeur paramétrique dans le processus de calcul séquentiel de la valeur suivante. Les fonctions polynomiales qui sont à la base des figures fractales reposent toutes sur le principe mathématique de la récursivité algébrique.

En résumé : le calcul séquentiel des valeurs numériques d'une fonction en boucle récursive se définit donc, opératoirement, par la réinjection ad libitum, à chaque étape du calcul en chaîne, de la valeur obtenue à l’étape précédente. L’évolution des valeurs numériques de la fonction (et par conséquent de la courbe géométrique qui lui est associée) est donc déterminée, à chaque étape, par la réutilisation systématique de la valeur numérique calculée en dernier. — Considérons, par exemple, des nombres réels et complexes particuliers Z et C (rappelons qu’un nombre complexe est du type [a + ib] où i² = −1), choisis initialement pour le calcul itératif de l’équation quadratique (Z² + C) ↔ Z, et l’algorithme de calcul récursif ci-après, typique du calcul séquentiel des valeurs numériques de certains ensembles fractals définis dans le plan complexe (les très populaires « ensemble de Mandelbrot » et « ensembles de Julia » en particulier) : (Z² + C)  →  Z  →  (Z² + C)  →  Z  →  (Z² + C)  →  Z  → … etc.

Cet algorithme en boucle récursive montre qu’à partir des valeurs Z et C fixées arbitrairement au départ : par exemple Z (réel) = 0,15 et C (complexe) = 1 − 3i, on obtient une nouvelle valeur de Z qui est immédiatement « réinjectée » dans l’équation pour le calcul de la valeur Z suivante ; puis cette valeur nouvelle est réutilisée à son tour pour le calcul suivant du nombre Z, et ainsi de suite, le paramètre C restant fixe au cours de ce processus de calcul récursif. La valeur initiale du nombre réel Z peut éventuellement être nulle (Z = 0). Il s’agit là d’un processus mathématique récursif d’autoréférence (ou d’auto-organisation) algébrique, simple par définition, l’algorithme « se nourrissant de lui-même » en quelque sorte.

5. Attracteurs étranges

L’évolution à moyen ou long terme d’un système dynamique peut conduire à des trajectoires dans l’espace physique – appelé « espace des phases » – complètement désordonnées et imprédictibles, dénuées de tout cycle périodique repérable : ce sont des « attracteurs étranges ». Ces trajectoires chaotiques, dites également « stochastiques » puisqu’elles mettent en jeu des processus dynamiques aléatoires (tout au moins supposés tels), ou plus généralement semi-aléatoires (engendrés par un programme déterministe), peuvent être considérées comme des attracteurs de période théoriquement infinie (il s’agit, bien entendu, d’une pseudo-période puisqu’elle n’est pas objectivement repérable).

Bien souvent, un système dynamique présentant, dans la phase initiale de son évolution, un ou plusieurs attracteurs de périodes données, peut évoluer brusquement vers un comportement complètement chaotique, caractéristique des attracteurs étranges. Ce type d’attracteurs est simulable sur ordinateur, au moyen de la programmation itérative d’équations non linéaires (comme celles servant à engendrer les images fractales autosimilaires). Il faut souligner également que les systèmes dynamiques complexes (physiques, chimiques et mathématiques, voire sociologiques) sont généralement très sensibles aux conditions initiales de leurs transformations spatio-temporelles (« effet papillon »), génératrices d’attracteurs étranges imprédictibles ou bien d’attracteurs cycliques (périodiques). Les figures géométriques complexes formées par les attracteurs étranges mêlent inextricablement le continu apparent (des quasi-lignes et des quasi-surfaces) et le discontinu (des simili-points, plus ou moins petits et denses). [↑ L'image fractale ci-dessus : Vue d'un Attracteur étrange à une échelle de résolution donnée, montrant l'imbrication inextricable du continu et du discontinu des trajectoires.]

6. Bassin d’attraction / Trajectoire de phase

Les déplacements continus caractéristiques des systèmes dynamiques physico-mathématiques, forment des trajectoires instables et complexes mais dont il est possible de faire la typologie. Ces trajectoires objectivement repérables sont des attracteurs formant des « bassins d’attraction ». De tels systèmes autoréférentiels, dont l’évolution dans l’espace des phases, à moyen et long terme, est simulable sur ordinateur, sont descriptibles en fonctions des types de bassins d’attraction – et donc des types d’attracteurs – qu’ils engendrent au cours du temps. On distingue les attracteurs stationnaires (un point fixe auquel aboutit le système), les attracteurs T-périodiques (obéissant à un cycle limite de période T), les attracteurs quasi-périodiques ou pseudo-périodiques (des cycles à peu près stables, mais avec deux ou plusieurs périodes alternantes), enfin les attracteurs apériodiques ou chaotiques, dits « attracteurs étranges » ou attracteurs stochastiques, car ils sont sous-tendus par des processus aléatoires.

Quand un système physique, mathématique ou même social évolue chaotiquement, sa transformation spatio-temporelle s’effectue de manière discontinue et souvent brusque, sans qu’il soit possible de prévoir à l’avance son évolution. L’ensemble des péripéties qui affectent l’évolution de ses paramètres plus ou moins nombreux est appelé « trajectoire de phase ». Il s’agit en somme des déplacements imprévisibles – objets d’évaluations probabilistes – qui régissent de manière complexe le devenir des constituants du système. Ces déplacements spatio-temporels sont de types morphologiques variés, et parviennent à former des « bassins d’attraction » périodiques plus ou moins stables dans le temps, ou même complètement chaotiques (apériodiques).

7. Auto-organisation

Capacité d’un système dynamique (physique, mathématique, biologique ou social) de se fixer par lui-même – de manière autotélique – ses règles et ses lois d’organisation et d’évolution au cours du temps. Le paradigme de l’auto-organisation apparaît au cours des années 1960-1970, entre autres chez Heinz Von Foerster, Henri Atlan, Ilya Prigogine, Edgar Morin. Il s’agit de penser des phénomènes complexes d’organisation spontanée, qui intègrent cependant dans cette auto-organisation créatrice d’ordre, des perturbations imprévisibles, facteurs de désordre, servant cependant à l’auto-organisation même du système. On parle alors d’organisation ou d’ordre par le « bruit », terme signifiant le hasard en théorie mathématique de l’information. L’expression « ordre par fluctuation » est aussi employée pour désigner la renaissance d’un ordre particulier à partir de phénomènes désordonnés, de nature aléatoire ou semi-aléatoire.

8. Chaos

La notion scientifique de « chaos » n’est pas du tout assimilable à l’absence d’ordre (le chaos primitif biblique, par exemple). Au contraire, le chaos possède ses lois propres, mais elles sont seulement appréhensibles au moyen de la statistique et du calcul des probabilités. Les lois du chaos sont indéterministes ou tout au moins semi-déterministes, c’est-à-dire qu’elles incluent une grande part de hasard. De nombreux phénomènes physico-chimiques, mais aussi économiques, sociologiques et biologiques, ne sont appréhensibles que par des lois probabilistes. Le concept de chaos désigne donc, de manière générale, un état du monde qui, pour la raison humaine déterministe, est inexplicable en dehors d’évaluations statistiques et probabilistes. D’autre part, bien que régi par des lois probabilistes, le chaos est parfois dit aussi déterministe ou semi-déterministe, pour signifier que les mécanismes qui l’engendrent sont, quant à eux, parfaitement connus et descriptibles. Ainsi, un algorithme informatisé qui engendre une image fractale, est en soi fort simplement descriptible, et agit selon un principe entièrement déterministe, bien que l’évolution de la fonction récursive qu’il commande demeure imprévisible à plus ou moins court terme, et que les images fractales offrent des structures évolutives très complexes.

9. Complexité / Entropie / Néguentropie

Dans le langage des sciences physico-mathématiques modernes, essentiellement depuis les années 1960 et 1970, la complexité n’est absolument pas synonyme de « complication » au sens ordinaire du mot, mais désigne un état de notre connaissance du monde, en ses innombrables composantes, qui prend en compte l’indéterminisme inhérent aux lois d’organisation des choses, ainsi que la relativité de notre connaissance approchée de ces choses. Aussi la théorie scientifique de la complexité fait-elle appel à des lois probabilistes destinées à fournir une connaissance seulement approchée (mais véridique) des phénomènes. La complexité d’un phénomène est souvent sans rapport avec les mécanismes initiaux qui l’engendrent. Par exemple, une image fractale hyperdétaillée et ramifiée à toute échelle de grandeur, présente un aspect apparemment très complexe, mais l’algorithme itératif déterministe qui l’engendre est parfaitement simple et descriptible, alors que les trajectoires de points de l’image fractale, mêlant inextricablement continuité (relative) et discontinuité à toute échelle d'exploration, ne sont pas prévisibles pour le programmeur informaticien.

Les concepts d'entropie et de néguentropie appartiennent à la théorie mathématique de l’information, formulée dans les années 1940-1950 par les ingénieurs-mathématiciens américains Claude Elwood Shannon (1916-2001) et Warren Weaver (1894-1978). L’entropie désigne l’état d’incertitude intellectuelle relative, dans lequel nous sommes à l’égard des états du monde. La néguentropie désigne au contraire, positivement, l’état de certitude qui nous permet de comprendre un phénomène. – Par extrension, le mot « entropie » signifie également l’état de désordre relatif d’une configuration ou d’un système, alors que le mot « néguentropie » signifie l’ordre particulier adopté, à un moment donné de son évolution spatio-temporelle, par une configuration ou un système. Ces concepts de théorie de l’information s'appliquent directement aux questions concernant les sciences de la complexité et les fractals, puisque les états évolutifs d'un système chaotique (comme les attracteurs étranges et les fractales non-linéaires) détiennent une entropie plus ou moins élevée, en fonction de leur degré d'imprévisibilité, autrement dit de leur complexité spatio-temporelle, laquelle peut varier en fonction des diverses échelles d'observation sélectionnées.

10. Déterminisme / Indéterminisme / Semi-déterminisme 

L’idée de déterminisme absolu désigne tout processus (physique, chimique, mathématique, humain) réglé intégralement par des lois connues, qui déterminent son évolution ou son devenir, étape après étape, en vertu d’une causalité implacable. Inversement, on parle d’indéterminisme quand il s’agit d’évoquer des phénomènes supposés être intégralement déterminés par le hasard, et dont seule une appréhension statistique et probabiliste peut rendre compte, en l’absence (parfois provisoire) de loi déterministe. Un processus est dit semi-déterministe quand il combine les deux caractéristiques précédentes : une part de hasard (supposé) et une part de déterminisme connu.

Les figures fractales et, en général, les figures du chaos propres aux systèmes dynamiques, répondent à des processus semi-déterministes, car d’une part elles résultent de la mise en œuvre d’algorithmes parfaitement connus, mais d’autre part leur complexité formelle, due aux calculs récursifs (en chaîne) qui les engendrent, interdit de se prononcer sur leur évolution morphologique à plus ou moins long terme. Elles sont, en particulier, « sensibles aux conditions initiales » (SCI) de la programmation, ce qui veut dire que deux paramètres numériques différents, mais éventuellement extrêmement proches l’un de l’autre en valeur absolue (par exemple, les valeurs décimales 0,1 et 0,1001 distinctes de 

1/10 000^è en valeur absolue), pourront engendrer éventuellement des trajectoires de points complètement divergentes. Ce phénomène est spécifique des fonctions non linéaires (ou récursives), telles que celles utilisées pour engendrer des images fractales.

11. Diamorphose / Morphogenèse

Processus d’engendrement continu d’images en transformation ou métamorphose permanente. Les images fractales font l’objet d’un calcul diamorphique de leurs structures hyperdétaillées, car elles s’autogénèrent informatiquement en permanence à diverses échelles d’exploration, et gagnent sans cesse en précision et finesse chromatique, par le processus calculatoire des points de l’image en restructuration infographique continue. De plus, elles sont mathématiquement combinables entre elles, de telle sorte que leur transformation continue (en deux ou trois dimensions) peut être indéfiniment renouvelée. — L'expression « morphogenèse » signifie littéralement le devenir continu d’une forme en auto-transformation. Les images fractales sont des formes en morphogenèse numérique permanente, par le jeu du calcul récursif de leurs points à toute échelle d’exploration sélectionnée. Ce terme est donc synonyme, dans le contexte de la fractalité, du mot « diamorphose ».

12. Mésoscopique

Entre l’infiniment grand et l’infiniment petit des mathématiciens et des physiciens, il existe une hiérarchie illimitée d’échelles d’examen gigognes (emboîtées) des phénomènes physico-mathématiques. Tout point de vue humain, même médiatisé par des instruments d’optique hyper-sophistiqués, demeure relatif à une certaine échelle d’observation, à jamais mésoscopique, c’est-à-dire intermédiaire entre des échelles d’observation plus grandes et plus petites qu’elle. Il n’existe pas d’échelle absolue qui serait la clé universelle de toute observation humaine. À ce titre, le point de vue mésoscopique marque l’incertitude relative, mais fondamentale, installée au sein de la conscience et de la connaissance humaines des choses de l’univers, y compris celles de l’être humain lui-même.

 © Jean-Claude Chirollet