Nuage fractal, point euclidien, détail pictural (2)
Du point euclidien au nuage fractal
Matrices génétiques du détail
2è partie
3. Du point euclidien à la « poussière de points fractale » de Cantor
Une telle prise en compte analytique du point et de la ligne géométriques euclidiens en tant que détails fondamentaux et originaires (radicaux) de la forme artistique, est aujourd’hui substantiellement prolongée et repensée, premièrement dans le champ de recherche propre à la géométrie fractale ─ dont le mathématicien Benoît Mandelbrot (1924-2010) est considéré à juste titre comme le père fondateur ─, et deuxièmement dans celui des arts fractalistes et de la complexité chaotique [1], dont les créateurs internationaux, essentiellement depuis les années 1980, ont tenté de redéfinir le champ sémantique – plus ou moins flou – des concepts de point, de ligne et de surface, dans le but de repenser le détail « radical », archétypal, des éléments de la création artistique. Cependant, bien avant Benoît Mandelbrot et ses « nuages de points fractals », le mathématicien allemand Georg Cantor (1845-1918) ─ sorte de « nouvel Euclide » en la matière ─ fut l’initiateur de la construction mathématique ad infinitum du « point fractal », symbole par excellence de la mise en abyme du détail, telle qu’elle est pensée et mise en œuvre par les artistes fractalistes internationaux depuis la seconde moitié du vingtième siècle.
Georg Cantor étudia en 1883 cet étrange objet mathématique : « l'ensemble triadique », baptisé également du nom évocateur de « poussière de Cantor ». Il s'agit d'un ensemble fractal de points infinitésimaux, généré à partir d’un segment de droite [AB] de longueur finie, sur l’intervalle fermé à valeurs réelles infinies non dénombrables [0, 1]. Rappelons, à ce propos, que l’ensemble des nombres réels sur l’intervalle fermé [0, 1] est infini non dénombrable, car il est équipotent à l’ensemble R des nombres réels tout entier. Il y a en effet autant de « points » dans l’intervalle [0, 1] que dans l’ensemble R tout entier. Le microsegment [0, 1] contient donc virtuellement, en quelque sorte, l'intégralité du macro-univers infiniment dense des nombres réels, répartis de manière ordonnée sur une ligne imaginaire continue, de longueur infinie, sans commencement ni fin.
Le générateur fractal de l'ensemble triadique de Cantor, indéfiniment répétitif, est plutôt simple: le segment de droite [AB] est découpé en 3 parties, égales à 1/3 chacune de la longueur totale [0, 1]. Le tiers médian est supprimé, seuls sont conservés les deux tiers latéraux. À cette première étape du générateur, il reste donc 2 segments (21) de longueur 1/3. L’opération de fragmentation est ensuite réitérée pour les tiers restants : à la deuxième étape, il reste 4 segments (22) de longueur égale à 1/32 = 1/9. Puis la fragmentation est réitérée à l’identique pour les segments restants : à la troisième étape, il reste 8 segments (23) de longueur égale à 1/33 = 1/27.
La fragmentation se poursuit en théorie indéfiniment. À la nè étape, il reste 2n segments de longueur égale à 1/3n, pour n aussi grand que l’on veut. Quand n « tend vers l’infini » (n → ∞), 1/3n tend vers 0, c’est-à-dire est extrêmement voisin de zéro, ou encore « approximativement égal » à zéro (1/3n ≈ 0). En poursuivant le raisonnement « à l'infini », il ne subsiste plus qu'une « poussière de points » infinitésimaux, dont la dimension fractale D vaut (log 2 / log 3) = 0,6309… Elle est 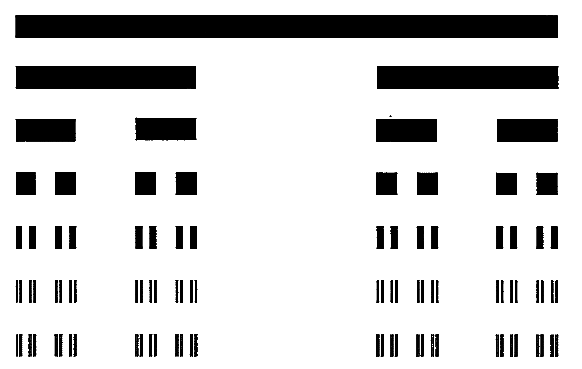 donc intermédiaire entre la dimension topologique du point (D = 0) et celle de la ligne idéalement mince et continue (D = 1), alors que le segment initial a pourtant été pulvérisé une infinité de fois [2]. La « poussière de points » ou le « nuage de points » – ou encore l’ensemble triadique – de Cantor, c’est précisément l’ensemble potentiellement infini des microsegments restants, obtenus par itérations successives ad infinitum, dont la somme : 2n/3n, est voisine de zéro (2n/3n ≈ 0 puisque 3n croît beaucoup plus vite que 2n), alors qu’il y a une infinité potentielle de microsegments. [Fig. 1 ci-dessus : Construction de la « poussière de points fractale » de Cantor, étapes 1 à 7.]
donc intermédiaire entre la dimension topologique du point (D = 0) et celle de la ligne idéalement mince et continue (D = 1), alors que le segment initial a pourtant été pulvérisé une infinité de fois [2]. La « poussière de points » ou le « nuage de points » – ou encore l’ensemble triadique – de Cantor, c’est précisément l’ensemble potentiellement infini des microsegments restants, obtenus par itérations successives ad infinitum, dont la somme : 2n/3n, est voisine de zéro (2n/3n ≈ 0 puisque 3n croît beaucoup plus vite que 2n), alors qu’il y a une infinité potentielle de microsegments. [Fig. 1 ci-dessus : Construction de la « poussière de points fractale » de Cantor, étapes 1 à 7.]
L’ensemble triadique de Cantor étant une « poussière de points » infinitésimaux, en nombre infiniment grand (non dénombrable), chaque microsegment – que nous dénommons « point fractal » par convention ad hoc – de l’ensemble triadique, quelle que soit son échelle de grandeur intermédiaire (mésoscopique), a donc une valeur numérique extrêmement proche de zéro, mais non nulle, puisqu’il est obtenu par l'itération indéfinie du générateur triadique. Les innombrables ordres de grandeur qui peuplent l'univers sans fond des nombres infiniment petits, peuvent ainsi être construits indéfiniment, par le jeu des emboîtements en cascade, à la manière d'une mise en abyme de micro-poupées gigognes. L'idée du point fractal cantorien n'est donc pas du tout semblable à celle du point topologique euclidien de dimension nulle (D = 0). Les « points » fractals cantoriens, dont l’ensemble est intermédiaire entre 0 et 1 (ici, D = 0,6309...), sont en quelque sorte des « quasi-riens » indéfiniment divisibles, et l’ensemble potentiellement infini de tous les microsegments infinitésimaux, est lui-même de dimension voisine de zéro, mais non nulle.
Il est possible d’appliquer, en théorie, d’innombrables autres générateurs fractals à la place du classique générateur triadique − notamment des générateurs aléatoires −, engendrant d’autres « poussières de points fractales » aux dimensions fractionnaires différentes, mais les ensembles pulvérisés qu’ils forment possèdent toujours une dimension fractale D comprise entre 0 et 1, intermédiaire entre le point euclidien « zéro-dimensionnel », et la ligne euclidienne idéalement mince, figure abstraite constituée de points en nombre infini, sans aucune épaisseur (D = 1). La notion de dimension non entière (fractionnaire) des objets fractals chaotise, en quelque sorte, le monde stable et régulier des objets géométriques euclidiens qui ne sont, tout compte fait, que des exceptions. C’est pourquoi elle s’applique si bien au monde des phénomènes naturels les plus variés, du microcosme au macrocosme.
En résumé : l'algorithme itératif de construction de la « poussière fractale » cantorienne pulvérise la ligne droite finie [AB], définie dans l'intervalle fermé à valeurs réelles [0, 1], en une infinité de « micro-points » – dénomination conventionnelle ad hoc –, correspondant eux-mêmes à une infinité potentielle d’échelles de grandeurs infinitésimales, emboîtées ad infinitum, de telle sorte qu’il engendre, paradoxalement, la quasi-vacuité – mais non le Rien ou le vide absolu –, avec du trop-plein, avec de l’excès, avec l’infini même en quelque sorte ! L'idée de « point fractal » retrouve par là-même une certaine forme de connotation intuitive, éliminée par la définition euclidienne du point sans partie, sans figure, de dimension nulle.
[1] Cf. Jean-Claude CHIROLLET, Art fractaliste – La complexité du regard, Paris, Éditions L’Harmattan, coll. Champs Visuels, 2005, et La question du détail et l’art fractal, Paris, Éditions L’Harmattan, coll. Histoires et Idées des Arts, 2011.
[2] Nous ne pouvons entrer, dans les limites de cet article, dans les arcanes de la théorie mathématique de la dimension d’un objet fractal, tel l’ensemble triadique de Cantor (il en existe potentiellement une infinité, possédant des dimensions fractales différentes selon leur principe de construction). C’est pourquoi nous donnons exclusivement les principes théoriques et les informations utiles sous l’angle de la seule différence entre les concepts de « point-détail » euclidien et celui de « point-détail » fractal. Par ailleurs, la littérature scientifique concernant les objets fractals, extrêmement abondante – y compris sur le Web –, s’étend de la vulgarisation élémentaire jusqu’aux niveaux mathématiques les plus pointus, concernant les seuls spécialistes.
4. Esthétique du détail fractal et du chaos
Le néologisme « fractal », utilisé par le mathématicien Benoît Mandelbrot dans la première édition française de son livre célèbre : Les Objets fractals – Forme, hasard et dimension [1], implique l'abandon du concept mathématique de symétrie spatiale [2] hérité de l’Antiquité grecque, qui est un concept fondamental de la géométrie euclidienne, au profit d'un autre type d'organisation – un « ordre chaotique [3] » – régissant, de manière dynamique et imprévisible, les formes spatiales irrégulières, morcelées et discontinues en tous leurs éléments, à toutes les échelles auxquelles elles sont appréhendées (dans l’espace plan, autant que dans l’espace tridimensionnel, simulé par ordinateur). Ce nouvel « ordre fractal » est défini au moyen d’un indice chiffré d'irrégularité morphologique, s’appliquant aussi bien aux objets de la nature qu’à ceux de la géométrie. Cet indice est la « dimension fractale », nombre absolu ne désignant pas une mesure de grandeur euclidienne au sens habituel, mais une mesure théorique (abstraite) de la complexité formelle des configurations infiniment ramifiées, brisées, irrégulières. Le participe passé latin « fractus » résume ces acceptions, en exprimant l'idée de moudre, de broyer et de fracturer.
Pour résumer à grands traits, intuitivement, l’idée-force qui sous-tend la pensée fractaliste, appliquée aussi bien à la géométrie pure qu’aux phénomènes complexes physiques ou humains les plus divers, on peut dire qu’en toute forme et tout phénomène observables ou analysables à de multiples (voire innombrables) échelles de grandeur, il existe une imbrication de détails morphologiques entrelacés, ramifiés, irréguliers, de micro-événements inextricables qui contiennent en puissance, en fonction de la pluralité des échelles d’examen, de plus en plus fines, auxquelles ils sont observés, une quantité innombrable d’autres détails inédits – parfois différents entre eux seulement d’un iota – qui émergent en cascade, par le jeu sans fin des « loupes de grossissement ». Le langage informatique évoque d’ailleurs, à propos des images fractales vidéonumériques, un processus de « magnification » fractale, terme provenant de l’anglais « to magnify » : amplifier, agrandir, accroître – l’expression anglaise « magnifying glass » désigne la loupe, le verre grossissant. En ce sens, le détail fractal est toujours une parcelle instable, provisoire, irrégulière, ouverte à la multiplication différenciatrice, à la prolifération incohérente des détails transitoires, révélés au gré des investigations instrumentées qui opèrent selon une multiplicité d’échelles.
Cette définition intuitive de la fractalité concerne, au sens strict, les formes fractales géométriques résultant de processus calculatoires semi-déterministes ou indéterministes (aléatoires), et non les figures fractales strictement déterministes (comme la courbe de Von Koch ou celle de Peano, par exemple), qui se répliquent mécaniquement à l’identique mais à plus petite échelle ou, inversement, à plus grande échelle, c’est-à-dire les fractales « scalantes » selon la terminologie de Mandelbrot. L’idée centrale de cette définition du fractal, c’est donc le processus indéfiniment réitéré de l’agrandissement en chaîne des détails de détails… etc., chaque micro-zone du plan géométrique, aussi infime (infinitésimale) soit-elle, contenant virtuellement une infinité de nouveaux détails irréguliers, inédits et imprévisibles, amplifiés par le calcul intensif de la magnification numérique.
Or, la notion de détail prise en compte sous l’angle élargi de la pensée fractaliste, fournit un cadre extensif à la conception du détail à l’intérieur du champ des diverses pratiques artistiques. Elle est considérablement enrichie par rapport à théorie classique du détail, car elle est plus compréhensive que la simple considération du rapport de la partie finie à l’ensemble, au « tout » non moins fini, fermé, clos sur lui-même, auquel elle appartient. Les artistes fractalistes internationaux des années 1980 aux années 2000, Carlos Ginzburg [4] en tête, ont bien compris, à cet égard, qu’explorer plastiquement l’univers baroque du détail pulvérisé, brisé, irrégulier, pouvait conduire le regard et la conscience à naviguer dans un labyrinthe sans fin de détails proliférants, repliés, enchevêtrés et ramifiés, dont les œuvres plastiques ne peuvent fournir qu’une approche matériellement limitée, mais symbolique de l’infinitude pluriscalaire qui caractérise le concept de fractal géométrique [5]. Le fractal, modèle de référence pouvant servir la pratique créatrice des artistes plasticiens ou numériciens (adeptes de l’imagerie et de la musique fractales), constitue une théorie féconde de la complexité gigogne et pluriscalaire du détail formel.
L’art fractaliste sous ses diverses variétés d’expression (arts plastiques, arts numériques, musique et même littérature) prend appui sur la géométrie des échelles d’observation multiscopiques, pour développer une esthétique des rapports chaotiques entre la totalité et les parties de l’œuvre, qui remet radicalement en question l’idée de totalité esthétique et d’unité de la composition. Les artistes fractalistes instaurent une relation perceptive incertaine, flottante, entre les fragments visuels (ou sonores, en musique fractale), et l’ensemble hypothétique, idéalement « achevé », dont ils font partie. Leurs œuvres induisent le sens de l’autosuffisance du détail, de sa valeur plastique autonome. La valeur esthétique attachée au fragment, à la parcelle – même peu remarquable –, apparaît de fait comme supérieure à celle de la « totalité unitaire » hypothétique, bien que spontanément supposée.
En ce sens, les créations fractales mettent en œuvre la nature mésoscopique inhérente à toute image du réel : le « microscopique » autant que le « macroscopique » demeurent pour toujours des intermédiaires entre des mondes infiniment plus petits qu’eux et des mondes infiniment plus grands. Aussi les artistes fractalistes dans leur ensemble – et notamment Carlos Ginzburg –, jouent-ils abondamment du zoom et de la parcellisation iconographique, en proposant au spectateur des niveaux échelonnés de perception visuelle. Ils invitent à observer de très près les détails de l’œuvre, selon une vision haptique [6] – littéralement : sur le modèle du toucher. Le regard proche devient actif, aigu, interrogateur ; une pluralité indéfinie d’échelles d’exploration se télescopent ou s’entrelacent. Inversement, les œuvres fractalistes incitent à reconstituer ad libitum une infinité potentielle d’ensembles formels plus ou moins unitaires, répondant au besoin spontané de totalisation psychique.
C’est donc une nouvelle et riche esthétique du détail qui naît de la comparaison entre, d’une part le détail artistique « ensembliste », significatif de la fonction euclidienne du détail dans l’art classique – la partie finie, fixe et hétéronome, rattachée à la loi unificatrice de l’ensemble clos –, et d’autre part le détail fractal – une particule, un « atome » qui recèle lui-même un univers d’atomes, de « poussières de points » et de quasi-lignes gigognes, infiniment repliés sur eux-mêmes, mais différenciés virtuellement ad infinitum. À titre méthodologique, après Mandelbrot – à la lumière du concept de complexité fractale –, il est devenu quasi impossible d’analyser globalement, et pour ainsi dire « à grande distance », les œuvres picturales anciennes ou contemporaines, uniquement comme si elles étaient des ensembles clos de signes figés, dont les détails interdépendants seraient insignifiants en eux-mêmes, subordonnés à la loi implacable de la composition par la pensée créatrice supposée homogène d’un artiste.
L’exigence cognitive de « creuser » toujours plus loin dans le cœur du visible, à l’exemple de la théorie géométrique du fractal, met le regardeur en quête continuelle de détails imprévisibles, qu’il engendre de toutes pièces par l’exercice même de son regard haptique instrumenté – loupes, photographie rapprochée, macrophotographie, reproductions en gros plan, agrandissements numériques, etc. –, sans pouvoir attribuer de seuil précis à la taille minimale du détail observable ou intéressant, estimé significatif. L’observateur attentif et interrogateur fait ressortir les détails, et plus encore les construit, en « détaillant » (au sens littéral) les œuvres picturales. Il en établit pour ainsi dire la « cartographie mobile », en fonction de divers modes de « découpage » des figures.
La dialectique perceptive des échelles d’observation s’exerce quasi continûment, du fragment « aléatoire » à l’ensemble instable, et vice-versa. On peut parler, à ce propos, d’une esthétique dynamique de la perception dialogique [7] des formes, allant sans cesse d’un niveau « micro » à un niveau « macro », et inversement, à travers le dédale des formes labyrinthiques de l’œuvre d’art. Une telle perception dialogique s’exerce, par exemple, quand le regard porte sur les formes entrelacées de l’art décoratif musulman traditionnel. Les parcours possibles du regard, à travers ces entrelacs de figures géométriques, suivent de manière erratique un véritable labyrinthe de formes complexes, une multiplicité de chemins tortueux, virtuellement infinis, toujours incertains, inconstants et précaires.
Bien avant l’époque de l’art fractal, Henri Focillon – déjà évoqué à propos de la géométrie euclidienne à la Renaissance – a su décrire en des termes déjà évocateurs de la géométrie fractale, ce caractère perceptif dialogique qui résorbe et exhume, alternativement, tous les détails d’une configuration plastique entrelacée à toute échelle d’observation, à propos de l’art décoratif musulman : « Qu’y a-t-il de plus éloigné de la vie, de ses flexions, de sa souplesse, que les combinaisons géométriques du décor musulman ? Elles sont engendrées par un raisonnement mathématique, établies sur des calculs, réductibles à des schémas d’une grande sécheresse. Mais dans ces cadres sévères, une sorte de fièvre presse et multiplie les figures ; un étrange génie de complication enchevêtre, replie, décompose et recompose leur labyrinthe. Leur immobilité même est chatoyante en métamorphoses, car, lisibles de plus d’une façon, selon les pleins, selon les vides, selon les axes verticaux ou diagonaux, chacune d’elles cache et révèle le secret et la réalité de plusieurs possibles. [8] »
Le regard flotte entre les échelles spatiales, il n’est jamais stable, jamais rassasié, toujours en attente, il éprouve les formes peintes comme des champs de forces dissymétriques, en tension alternative, il « zoome » continuellement et de manière discontinue, entre « macro » et « micro ». Carlos Ginzburg a décrit de manière poétique cette errance du regard « en boucle rétroactive infinie », ainsi que ces champs de forces dissymétriques, éprouvés par le spectateur attentif de ses œuvres fractales, en un texte intitulé Le Zoom de l’Astronaute :
« Mes œuvres semblent être comme ces îles volantes, des signes en flottaison dans l’espace vide, un univers virtuel hors sol, décroché de toute réalité ou territoire ; des champs de forces en voie d’actualisation. L’observateur flotte aussi dans l’espace et voit d’en haut : il occupe la place de l’astronaute en mouvement et/ou en téléportation. Que ce soit dans une même œuvre ou dans le passage d’une œuvre à une autre, on opère des zooms discontinus. On voit de loin de grandes taches colorées reliées par le réseau, puis, presque instantanément, on voit de tout près une multitude de détails qui apparaissent avec des histoires conceptuelles, picturales, etc.…. Puis, tout s’évanouit pour recommencer dans une boucle rétroactive infinie. [9] »
 En somme, une œuvre fractaliste à l’instar de celles créées par Carlos Ginzburg depuis les années 1980, est exhaustivement constituée de détails autonomes, dans la mesure où la vision d’ensemble n’offre plus aucune cohésion compositionnelle. Le détail règne en maître, il est omniprésent, au gré de la découpe, de la « détaille » ad libitum du regard haptique (détail-dettaglio). Il s’agit là d’un modèle de création artistique totalement opposé à la thèse classique de l’hétéronomie du détail, lequel ne prend son sens véritable que des seules règles unifiantes de la composition d’ensemble (détail-particolare) [10]. [Fig. 2 ci-dessus : Carlos Ginzburg, La subjectivité fractale, 2005, détail, technique mixte, l’ensemble : 100 × 75 cm.]
En somme, une œuvre fractaliste à l’instar de celles créées par Carlos Ginzburg depuis les années 1980, est exhaustivement constituée de détails autonomes, dans la mesure où la vision d’ensemble n’offre plus aucune cohésion compositionnelle. Le détail règne en maître, il est omniprésent, au gré de la découpe, de la « détaille » ad libitum du regard haptique (détail-dettaglio). Il s’agit là d’un modèle de création artistique totalement opposé à la thèse classique de l’hétéronomie du détail, lequel ne prend son sens véritable que des seules règles unifiantes de la composition d’ensemble (détail-particolare) [10]. [Fig. 2 ci-dessus : Carlos Ginzburg, La subjectivité fractale, 2005, détail, technique mixte, l’ensemble : 100 × 75 cm.]
[1] Benoît MANDELBROT, Les Objets fractals – Forme, hasard et dimension, 1è éd. 1975, 4è éd. revue 1995, Paris, Flammarion.
[2] La « symétrie », au sens euclidien du terme grec, désigne la commune mesure entre deux ou plusieurs grandeurs, que le géomètre peut donc comparer avec la même unité de référence : l’unité de mesure commune. Ainsi, on peut comparer les dimensions de deux (ou plusieurs) murs, ou de deux (ou plusieurs) portes, au moyen d’une seule mesure de grandeur commune : le mètre-étalon, ou l’une de ses subdivisions, le décimètre (10 cm) par exemple. Les grandeurs, ainsi obtenues par comparaison avec l’unité de mesure de référence commune – qui sont donc de même nature (longueurs spatiales) –, sont dites « symétriques », sans aucune considération d’échelle d’examen.
[3] La notion scientifique de « chaos » ne signifie pas l’absence d’ordre. Au contraire, le chaos possède ses lois propres, seulement appréhensibles de manière statistique et probabiliste. Les lois du chaos sont indéterministes : elles incluent une grande part de hasard. De nombreux phénomènes physico-chimiques, économiques, sociologiques, biologiques, etc., ne sont appréhensibles que par des lois probabilistes. Le concept de chaos désigne donc, de manière générale, un état du monde inexplicable en dehors d’évaluations statistiques et probabilistes. D’autre part, bien que régi par des lois probabilistes, le chaos est souvent dit « déterministe » ou « semi-déterministe », pour signifier que les mécanismes qui l’engendrent sont parfaitement connus. Ainsi, un algorithme récursif (itération indéfinie) qui engendre une image fractale, est en soi fort simplement descriptible. Il agit selon un principe entièrement déterministe, bien que l’évolution de la fonction récursive qu’il commande demeure imprévisible, à l’origine d’images fractales morphologiquement très complexes, explorables à une infinité (potentielle) d’échelles de grandeur.
[4] Carlos GINZBURG – né en 1946 à La Plata en Argentine, il vit à Paris (France) –, artiste et théoricien du fractal, développe depuis le tout début des années 1980 une œuvre artistique fractaliste variée de vaste envergure, en continuel renouvellement. Son œuvre à plusieurs facettes, ancrée dans une forte conception philosophique fractaliste de l’art, de la société et de la mondialisation, est une référence historique majeure au sein du mouvement fractaliste international.
[5] Cf. Jean-Claude CHIROLLET, Art fractaliste – La complexité du regard, Paris, Éditions L’Harmattan, coll. Champs Visuels, Paris, 2005 et La question du détail et l’art fractal, Paris, Éditions L’Harmattan, coll. Histoires et Idées des Arts, 2011.
[6] Le terme d’origine grecque « haptique » désigne le sens tactile, ce qui concerne les sensations relatives au toucher.
[7] L’idée de « dialogique », introduite par le théoricien russe de la littérature Mikhaïl BAKHTINE (1895-1975), reprise comme un leitmotiv par le sociologue et philosophe français de la complexité Edgar MORIN (né en 1921), désigne la multiplicité des logiques, irréductibles entre elles, qui œuvrent en alternance ou en interaction, dans tout processus de pensée, et, au-delà, dans toute conduite humaine individuelle ou collective.
[8] Henri FOCILLON, Vie des formes, 1è éd. 1943, Paris, P.U.F., 2004, p. 9. – Henri Focillon reconnaît des caractères morphodynamiques analogues dans l’art de la sculpture romane.
[9] Carlos GINZBURG, Le Zoom de l’Astronaute, 2001, in Jean-Claude CHIROLLET, La question du détail et l’art fractal, Paris, Éditions L’Harmattan, coll. Histoires et Idées des Arts, 2011, p. 52.
[10] La distinction du détail-particolare et du détail-dettaglio fait ici référence aux écrits de Daniel Arasse à ce sujet. Cf. Daniel ARASSE, Le Détail – Pour une histoire rapprochée de la peinture, 1è éd. Paris, Flammarion, 1992, rééd. actualisée Flammarion, Paris, 2008. Édition de poche Paris, Champs/Flammarion, 1996 et 2009. Cf. aussi Daniel ARASSE, Histoires de peintures, Paris, Édition France Culture/Denoël, 2004, rééd. Paris, Gallimard, coll. folio/essais, 2006. – Cf. notre discussion de cette distinction faite par ARASSE in : Jean-Claude CHIROLLET, La question du détail et l’art fractal, Paris, Éditions L’Harmattan, coll. Histoires et Idées des Arts, 2011, Chapitre VI-2, p. 212-226.
5. Espace euclidien vs Espace fractal : matrices génétiques du détail
Au terme de cette réflexion sur le passage du point euclidien, condition radicale du détail dans l’œuvre plastique classique, au « nuage fractal » en tant que principe d’émergence chaotique des formes plastiques ou numériques en genèse continue, dont les « détails » irréguliers demeurent à jamais transitoires, instables, il convient de s’interroger sur le statut ontologique des deux types d’espaces géométriques hétérogènes qui conditionnent, à travers leur différence, le sens du détail en art : l’espace de la géométrie euclidienne et celui de la géométrie fractale. Aristote, comme il a été dit au début de cet article, n’a pas conçu le point géométrique – qui est un objet mathématique : le sêméion d’Euclide –, mais seulement la « piqûre » (stigmé), trace spatiale d’une inscription matérielle. Cependant, il évoque dans la Métaphysique (A, 9, 992a, 19-24) l’opinion que Platon aurait défendue, selon lui, à propos de la notion de « point » : « En outre, d’où les points contenus dans la ligne procéderont-ils ? Platon lui-même combattait la notion de point comme n’étant qu’une conception géométrique, mais il l’appelait "principe [générateur] de la ligne", et il se servait même souvent de l’expression "lignes insécables". Cependant, il faut bien que ces lignes insécables aient une limite ; aussi l’argument qui établit l’existence de la ligne insécable établit-il aussi celle du point. [1] »
Aristote attribue à Platon une conception du point comme principe générateur des figures du plan, et non comme figure géométrique proprement dite ; le « point » est l’origine ou le principe dynamique (archè) des lignes tracées par le géomètre. En ce sens, cette opinion est analogue à celle qu’Euclide produira dans les Éléments : « le point est ce qui n’a pas de partie » (L. I, Déf. 1). Or, en mettant l’accent sur le caractère générateur du point – fiction géométrique –, Aristote souligne implicitement le fait que la géométrie mathématique est la construction abstraite d’un espace matriciel, à partir duquel sont engendrées toutes les grandeurs physiquement inscriptibles et calculables du géomètre. C’est précisément le cas des Éléments de géométrie d’Euclide, à partir desquels les artistes de diverses époques, mais en particulier à la Renaissance, ont pensé et mis en pratique le sens du détail pictural, ainsi que nous l’avons expliqué dans la deuxième partie de cet article. L’espace euclidien est une sorte de matrice génétique du détail artistique.
Quant à l’espace propre à la géométrie fractale, il représente un autre type de matrice génétique du détail, dont s’inspirent les artistes fractalistes depuis les années 1980, en privilégiant la luxuriance, l’instabilité et l’irrégularité multiscalaire ad infinitum du détail. Ces deux types d’espaces matriciels – qui suggèrent un sens possible de la « khôra » (χωρα) platonicienne du Timée – sont à l’origine de deux conceptions, antithétiques, de la fonction esthétique du détail dans les arts visuels.
[1] Aristote, La Métaphysique, A, 9, 992a, 20-24, Paris, Librairie Philosophique J. Vrin, Tome I, 1974, p. 96-97.
© Jean-Claude Chirollet
