Fractals semi-déterministes (hyperfractals) / Autosimilarité
Il est conseillé de renforcer la luminosité de l'écran, afin de révéler plus nettement les détails des images fractales, obtenues au moyen de générateurs mathématiques.
1. Systèmes dynamiques, hyperfractals, autosimilarité
Les objets fractals les plus complexes, appelés « multifractals » ou « hyperfractals », dotés de la propriété d’autosimilarité – les plus riches en irrégularité et différences morphologiques –, proviennent de systèmes dynamiques semi-déterministes, dont les trajectoires, calculées point par point en boucle récursive, génèrent des formes semi-aléatoires hyperdétaillées à toute échelle − par exemple, le « bonhomme fractal » de  Mandelbrot (ou « ensemble de Mandelbrot »), le plus connu parmi d’innombrables fractales dynamiques. Une image fractale calculée à une certaine échelle d’exploration avec le « microscope informatique », recèle une extrême densité de détails chaotiques, caractérisés par des dimensions très voisines statistiquement à cette échelle. Les innombrables images « multifractales », statistiquement autosimilaires, générées par des algorithmes récursifs (itération ad infinitum), peuvent être recalculées indéfiniment en chacun de leur point, pour produire des zooms numériques illimités. [→ Image ci-contre : Vue de l'ensemble de Mandelbrot.]
Mandelbrot (ou « ensemble de Mandelbrot »), le plus connu parmi d’innombrables fractales dynamiques. Une image fractale calculée à une certaine échelle d’exploration avec le « microscope informatique », recèle une extrême densité de détails chaotiques, caractérisés par des dimensions très voisines statistiquement à cette échelle. Les innombrables images « multifractales », statistiquement autosimilaires, générées par des algorithmes récursifs (itération ad infinitum), peuvent être recalculées indéfiniment en chacun de leur point, pour produire des zooms numériques illimités. [→ Image ci-contre : Vue de l'ensemble de Mandelbrot.]
Chaque détail obtenu au cours du processus de calcul itératif, peut donner lieu indéfiniment à de nouvelles explorations en cascade (« effet-zoom » à l'infini), selon des échelles de grandeur toujours inférieures. De nouveaux microdétails fractals « inclus dans le détail », apparaissent en chaîne à chaque exploration scalaire nouvelle, révélant à chaque fois une minuscule copie, mais légèrement déformée, de la forme originale. Chaque réplique est donc toujours originale du point de vue morphologique, par sa légère différence de dimension fractale, bien que globalement analogue à la forme primitive d’où elle provient. Il s’agit de la propriété géométrique appelée, par simplification, « invariance d’échelle ».
Il serait cependant plus juste de parler d’invariance dimensionnelle générale ou de structurale globalement invariante par le jeu des changements d’échelles en série, puisque tout changement d’échelle d’examen révèle une invariance morphologique générale (caractérisée par son unique dimension fractale D), mais à de petites transformations locales près. Il s'agit là précisément, de la propriété d'autosimilarité fractale qui caractérise les fractals semi-déterministes (fractals « chaotiques ») engendrés par le processus algorithmique de renormalisation ad infinitum. C'est pourquoi les formes fractales semi-déterministes opèrent leurs transformations à l'intérieur d'un univers illimité d'ordres de grandeur gigognes et hétérogènes, caractéristique des systèmes de nombres non-archimédiens : les nombres hyperréels utilisés en Analyse Non-Standard.
La fractalité chaotique, de nature statistique, instaure par conséquent une dialogique inédite entre le local et le global, qui inspire substantiellement la majorité des artistes fractalistes, depuis les années 1980. Les fractals semi-déterministes – ou « hyperfractals » –
reposent sur une part importante de complexité aléatoire, car si les algorithmes informatiques mis en œuvre sont entièrement déterministes, en revanche les trajectoires de points résultant des calculs itératifs sont imprévisibles à plus ou moins long terme, en fonction des paramètres algébriques choisis au départ du processus de calcul des points dans le plan complexe. Les figures fractales répondent à leur façon au principe de non-localité, défini par la physique quantique, car leur structure locale demeure incertaine, instable et transitoire, en fonction des interactions imprévisibles entre les paramètres algébriques mis en jeu dans les calculs itératifs.
Rappelons, si nécessaire, que le plan complexe est l’ensemble infini (infini non dénombrable) des couples de nombres de coordonnées réelles (a,b), représentant tous les points du plan au sein d’un repère géométrique orthonormé. Possédant leurs règles spécifiques de calcul algébrique, les nombres complexes s’écrivent sous la forme générale : (a + ib), où i² = -1. Le nombre "a" est la partie réelle ; le nombre "ib" est la partie imaginaire (exemple : 5 + 7i). Le corps algébrique C des nombres complexes est une extension du corps algébrique R des nombres réels. À ce titre, ils ont des propriétés mathématiques différentes de ces derniers. Les fonctions récursives servant à calculer les images fractales, sont formées de nombres complexes de ce type. D'autre part, entre deux nombres complexes – couples de réels (a,b) –, aussi voisins soient-ils dans  le plan, il existe une infinité potentielle d’autres nombres complexes (a,b). C’est pourquoi le « microscope numérique » peut s’exercer à une infinité d’échelles potentielles.
le plan, il existe une infinité potentielle d’autres nombres complexes (a,b). C’est pourquoi le « microscope numérique » peut s’exercer à une infinité d’échelles potentielles.
L’invariance morphologique globale des fractales semi-déterministes, caractérisée par une dimension fractale spécifique D, définit l’autosimilarité fractale par renormalisation, terme qui désigne un processus itératif de calcul des points d’une même zone du plan complexe, selon une infinité d’échelles potentielles de plus en plus fines, donc avec des grossissements informatiques de plus en plus élevés (zooms numériques successifs). Lorsque le calcul itératif est arrêté à un certain stade de la programmation (au bout de dix mille ou vingt mille étapes, par exemple), tous les détails pour cette échelle peuvent alors être à nouveau recalculés à des échelles inférieures, révélant de nouveaux détails imprévisibles. À leur tour, ces nouveaux fragments pourront devenir des terrains d’exploration infographique pour de multiples autres agrandissements, et ainsi de suite indéfiniment. Le plan complexe, gigantesque tableau de nombres hyperdenses, recèle une luxuriance morphologique virtuellement infinie, révélée progressivement par l'émergence inédite des fractales autosimilaires.
L’autosimilarité fractale est aussi appelée autosimilarité stochastique (ou statistique), car elle met en jeu l’idée de hasard semi-déterministe. Soulignons encore, afin d'éviter toute confusion, que les fractals semi-déterministes – dits « multifractals » ou encore « hyperfractals » –, simulant l’aléatoire, possèdent la propriété d’autosimilarité statistique, à ne pas confondre avec le concept d’autosimilitude (ou auto-identité) qui caractérise les fractales géométriques purement déterministes, dont toute partie réplique exactement le tout à n’importe quelle échelle d’observation, avec une unique et invariante dimension fractale, comme la courbe en « flocon de neige » de Von Koch, ou l’ensemble triadique de Cantor (« poussière de points » fractale), par exemple.
Par différence avec les hyperfractals semi-déterministes, les fractals entièrement déterministes, comme le « flocon de neige » de Von Koch, présentent une invariance d’échelle stricte, à la fois globale et locale, car tout détail y réplique exactement à l’identique, le tout à partir duquel il est construit, seule l’échelle de grandeur varie. Il s’agit de la « loi d’homothétie interne » des fractales auto-identiques, selon l’expression de Benoît Mandelbrot.
Dans la nature physique, cependant, les niveaux d’observation ne sont pas réellement infinis, à la différence d’un fractal mathématique (objet géométrique), qui peut être étudié selon des niveaux scalaires virtuellement infinis. Néanmoins, dans la pratique informatique du calcul dynamique des fractals géométriques en boucle récursive, on retrouve des limites physiques inexorables, dues aux contraintes techniques liées au temps et à la rapidité de calcul des microprocesseurs, ainsi qu'à la capacité de mémoire informatique disponible (nécessairement finie).
2. Gaston Julia et Pierre Fatou
Déjà, dans les années 1915-1920, les travaux des mathématiciens français Gaston Julia (1893-1978) et Pierre Fatou (1878-1929), relatifs au calcul récursif (itération)appliqué aux fonctions algébriques du second degré (fonctions quadratiques), avaient permis de relier la théorie de la dimension fractale à la science des systèmes dynamiques. Julia et Fatou ont démontré, en particulier, qu’il est possible d’engendrer par récursion algorithmique, des trajectoires géométriques dans le plan complexe qui  traduisent une imbrication subtile, imprévisible à plus ou moins long terme, d’ordre et de chaos. Or, de tels systèmes géométriques – fondés sur des équations quadratiques ou de degré supérieur – conduisent à décrire des valeurs dimensionnelles non entières (c'est-à-dire fractales), localisées irrégulièrement dans le plan (ou l’espace) complexe.
traduisent une imbrication subtile, imprévisible à plus ou moins long terme, d’ordre et de chaos. Or, de tels systèmes géométriques – fondés sur des équations quadratiques ou de degré supérieur – conduisent à décrire des valeurs dimensionnelles non entières (c'est-à-dire fractales), localisées irrégulièrement dans le plan (ou l’espace) complexe.
Les travaux mathématiques de Julia et Fatou sur l’itération indéfinie des polynômes algébriques dans le plan complexe, ont fourni une solide base théorique aux concepts qui sous-tendent la technoscience des figures fractales. D’ailleurs, les innombrables « ensembles (fractals) de Julia », obtenus aujourd’hui par ordinateur, sont considérés comme apparentés morphologiquement (c'est-à-dire quant à leurs propriétés géométriques), en leurs infinis détails, à l’ensemble fractal de Mandelbrot (dit « Bonhomme de Mandelbrot »), à partir duquel ils sont dérivés et calculés. [↑ Image ci-dessus : vue schématique d'un ensemble de Julia connexe.]
3. Jean Perrin
Dans son livre fondateur de la physique moderne, Les Atomes (1913), le physicien
français Jean Perrin (1870-1942), prix Nobel de physique en 1926 pour ses travaux sur la structure discontinue de la matière, fit remarquer l'importance majeure que revêt l'échelle d'observation des phénomènes naturels, pour la mise en évidence de la structure infiniment irrégulière de la matière, en particulier de son mouvement brownien.  Le monde physique n'est, en tous ses détails, qu'irrégularité, fracture, brisure, en n'importe quel sens de l'espace tridimensionnel. De l'infiniment petit à l'infiniment grand, conçus et représentés abstraitement par le mathématicien et le physicien, la discontinuité s'affirme comme la règle structurale universelle de l'organisation de l'Univers.
Le monde physique n'est, en tous ses détails, qu'irrégularité, fracture, brisure, en n'importe quel sens de l'espace tridimensionnel. De l'infiniment petit à l'infiniment grand, conçus et représentés abstraitement par le mathématicien et le physicien, la discontinuité s'affirme comme la règle structurale universelle de l'organisation de l'Univers.
Aussi Jean Perrin proposa-t-il, de manière prémonitoire, une vision scientifique éminemment fractaliste de l'Univers entier, dans la préface de son ouvrage publié en 1913 : « Une matière indéfiniment discontinue, trouant par des étoiles minuscules un éther continu, voilà donc l’idée qu’on pourrait se faire de l'Univers. [...] nous pourrions le dire en songeant à une sphère sans cesse élargie, englobant successivement planète, système solaire, étoiles, nébuleuses. Et nous retrouverions l’impression, devenue familière, que traduisait Pascal lorsqu’il nous montrait l’Homme "suspendu entre deux infinis". » (Jean Perrin, Les Atomes, 1913, Gallimard, Paris, 1970, p. 21-22, rééd. Champs/Flammarion, Paris, 1991, p. 31-32).
4. Blaise Pascal et Gottfried Wilhelm Leibniz
À la fin de ce passage, Jean Perrin fait allusion au texte célèbre des Pensées du philosophe et mathématicien Blaise Pascal (1623-1662 ; les Pensées ne furent publiées qu'en 1670), concernant les « deux infinis », c’est-à-dire, dans le langage du philosophe, l’infiniment petit et l’infiniment grand conçus par le mathématicien et le physicien. Quand l’homme contemple les objets de son environnement naturel, son regard sensible est très vite relayé par son imagination, car notre vue épuise rapidement ses capacités d’observation, aussi bien dans le champ de l’immensité que dans celui de l’infime. C’est l’imagination qui nous fait dépasser les limites de l’observation. Cependant, même l’imagination la plus fertile ne parviendra jamais à concevoir clairement l’infinité des univers invisibles qui s’emboîtent les uns dans les autres, aussi bien dans l’ordre du macrocosme que dans celui du microcosme. Les échelles de grandeurs qui régissent la nature sont illimitées et à jamais mésoscopiques – l’absolument petit ou l’absolument grand n’existent pas –, de telle sorte qu’aucun repère ne peut définir le centre de l’Univers : celui-ci est « une sphère infinie dont le centre est partout, la circonférence nulle part. » (Blaise Pascal, Pensées, § 72 de l’édition Léon Brunschvicg, Éditions GF-Flammarion, Paris, 1976, p. 65).
De même que l’Univers, pour le cosmologiste, n’a pas de terme concrètement assignable, la matière n’a pas, pour le physicien, de partie ultime, à l’instar des nombres entiers divisibles indéfiniment, pour l’éternité, sans que l’on puisse aboutir à un résultat strictement égal à zéro, au rien absolu. La division du nombre 1 par un nombre quelconque (aussi grand soit-il), réalisée de manière répétitive indéfiniment, n’aboutira jamais au zéro absolu, et tout nombre très petit ainsi obtenu au bout d’un très grand nombre d’étapes, restera toujours « immense » par rapport au nombre beaucoup plus petit, obtenu au bout d’une suite encore plus longue de divisions en chaîne. Les entités indivisibles n’ont aucune espèce de réalité, pas plus du point de vue mathématique que du point de vue physique, soutient Blaise Pascal dans un bref traité de philosophie mathématique intitulé De l’esprit géométrique (vers 1657-1658, Section I).
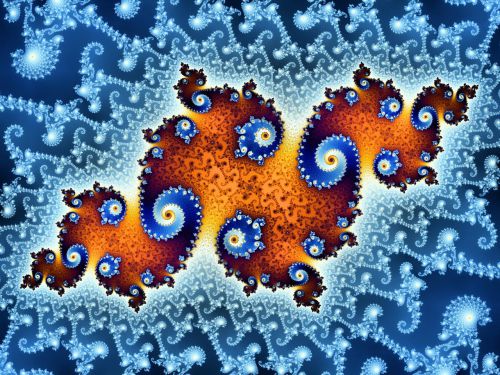 Dans ce petit traité de philosophie des mathématiques, Pascal explique qu’on peut toujours concevoir un mouvement indéfiniment plus rapide ou plus lent, sans aucun terme ultime (la vitesse absolue ou, inversement, le repos absolu). On peut également toujours concevoir un espace infiniment plus petit ou plus grand que n’importe quel espace imaginable, aussi petit ou immense que l’on voudra, sans jamais atteindre un espace indépassable en grandeur, ni indivisible dans sa petitesse. Le même raisonnement s’applique au temps : impossible de concevoir une temporalité ultime, aussi grande soit-elle, ni, inversement, un instant absolu sans aucune durée. La divisibilité potentiellement indéfinie du nombre offre, selon Pascal, le modèle mathématique par excellence de l’inexistence des indivisibles : « De même, quelque grand que soit un nombre, on peut en concevoir un plus grand, et encore un qui surpasse le dernier ; et ainsi à l’infini, sans jamais arriver à un qui ne puisse plus être augmenté. Et au contraire, quelque petit que soit un nombre, comme la centième ou la dix-millième partie, on peut encore en concevoir un moindre, et toujours à l’infini, sans arriver au zéro ou néant. » (Pascal, De l’esprit géométrique, éditions GF-Flammarion, Paris, 1985, p. 76). [↑ Image ci-dessus : fractale numérique d'un ensemble de Julia connexe.]
Dans ce petit traité de philosophie des mathématiques, Pascal explique qu’on peut toujours concevoir un mouvement indéfiniment plus rapide ou plus lent, sans aucun terme ultime (la vitesse absolue ou, inversement, le repos absolu). On peut également toujours concevoir un espace infiniment plus petit ou plus grand que n’importe quel espace imaginable, aussi petit ou immense que l’on voudra, sans jamais atteindre un espace indépassable en grandeur, ni indivisible dans sa petitesse. Le même raisonnement s’applique au temps : impossible de concevoir une temporalité ultime, aussi grande soit-elle, ni, inversement, un instant absolu sans aucune durée. La divisibilité potentiellement indéfinie du nombre offre, selon Pascal, le modèle mathématique par excellence de l’inexistence des indivisibles : « De même, quelque grand que soit un nombre, on peut en concevoir un plus grand, et encore un qui surpasse le dernier ; et ainsi à l’infini, sans jamais arriver à un qui ne puisse plus être augmenté. Et au contraire, quelque petit que soit un nombre, comme la centième ou la dix-millième partie, on peut encore en concevoir un moindre, et toujours à l’infini, sans arriver au zéro ou néant. » (Pascal, De l’esprit géométrique, éditions GF-Flammarion, Paris, 1985, p. 76). [↑ Image ci-dessus : fractale numérique d'un ensemble de Julia connexe.]
Il en résulte que les échelles de grandeurs, en mathématiques tout comme dans la nature, demeurent à jamais mésoscopiques, et l’homme est à la fois minuscule au sein de l’Univers, mais gigantesque par rapport à la constitution atomique de la matière : l’être humain se situe de manière incertaine « entre ces deux abîmes de l’infini et du néant […] Car enfin, qu’est-ce que l’homme dans la nature ? Un néant à l’égard de l’infini, un tout à l’égard du néant, un milieu entre rien et tout. » (Blaise Pascal, Pensées, § 72 de l’édition Léon Brunschvicg, éditions GF-Flammarion, Paris, 1976, p. 66).
Le thème pascalien de la constitution de la nature selon une infinité d’échelles de grandeurs emboîtées l’une dans l’autre, renvoie à l’idée de la structure fractale de l’Univers et de l’être humain, en vertu de laquelle toute portion de matière, aussi minuscule soit-elle, recèle une infinité d’univers semblables entre eux, bien que différents en tous leurs détails. Le fameux passage de Pascal sur le « ciron » – animalcule microscopique, sorte d’acarien invisible à l’œil nu –, dans le même paragraphe des Pensées, est révélateur d’une telle conception fractaliste de l’Univers. Un animalcule de cette sorte, malgré son extrême petitesse qui le rend invisible sans l’aide du microscope, contient en lui-même une infinité d’univers immenses et fort complexes. Un « simple » ciron est à lui seul un véritable labyrinthe de complexité, composé d’innombrables détails disposés en abyme par autosimilarité (fractale), selon des lois qui reflètent la structure de l’Univers entier.
Dans un minuscule ciron, le philosophe naturaliste pourra observer, grâce à la perspicacité de son esprit analytique, « une infinité d’univers, dont chacun a son firmament, ses planètes, sa terre, en la même proportion que le monde visible ; dans cette terre, des animaux et enfin des cirons, dans lesquels il retrouvera ce que les premiers ont donné ; et trouvant encore dans les autres la même chose sans fin et sans repos, qu’il se perde dans ces merveilles, aussi étonnantes dans leur petitesse que les autres par leur étendue. » (Blaise Pascal, Pensées, § 72 de l’édition Léon Brunschvicg, éditions GF-Flammarion, Paris, 1976, p. 66). L’infiniment grand – l’immensité de la nature – est enchâssé dans l’infiniment petit de la moindre parcelle microscopique de matière… Le local infinitésimal s’inverse, à tout moment et simultanément, en global infiniment grand, et vice-versa.
 De son côté, dans La Monadologie (1714), notamment aux paragraphes 65 à 68, Leibniz (1646-1716) avait conçu en termes relevant d’intuitions typiquement fractalistes, la surdétermination morphologique du chaos fractal, jusque dans les moindres replis microscopiques de la matière animée : « Chaque portion de la matière peut être conçue comme un jardin plein de plantes, et comme un étang plein de poissons. Mais chaque rameau de la plante, chaque membre de l’animal, chaque goutte de ses humeurs est encore un tel jardin, ou un tel étang (§ 67). Et quoique la terre et l’air interceptés entre les plantes du jardin, ou l’eau interceptée entre les poissons de l’étang, ne soit point plante, ni poisson, ils en contiennent pourtant encore, mais le plus souvent d’une subtilité à nous imperceptible (§ 68). » (Leibniz, La Monadologie, 1714, Librairie Générale Française, Paris, 1991, p. 163).
De son côté, dans La Monadologie (1714), notamment aux paragraphes 65 à 68, Leibniz (1646-1716) avait conçu en termes relevant d’intuitions typiquement fractalistes, la surdétermination morphologique du chaos fractal, jusque dans les moindres replis microscopiques de la matière animée : « Chaque portion de la matière peut être conçue comme un jardin plein de plantes, et comme un étang plein de poissons. Mais chaque rameau de la plante, chaque membre de l’animal, chaque goutte de ses humeurs est encore un tel jardin, ou un tel étang (§ 67). Et quoique la terre et l’air interceptés entre les plantes du jardin, ou l’eau interceptée entre les poissons de l’étang, ne soit point plante, ni poisson, ils en contiennent pourtant encore, mais le plus souvent d’une subtilité à nous imperceptible (§ 68). » (Leibniz, La Monadologie, 1714, Librairie Générale Française, Paris, 1991, p. 163).
© Jean-Claude Chirollet
