Arts / Numérisation / Fractals

« La nature s’invente, quelle que soit l’échelle,

du plus petit flocon à la tempête de neige »

(Tom Stoppard, Arcadia, Acte I, scène 4,

éd. Actes Sud-Papiers, p. 58)

Note préliminaire : les références à la pièce de théâtre de Tom Stoppard (né en Tchécoslovaquie en 1937), Arcadia (1993), sont données ci-dessous à partir de l’édition de cette pièce traduite et adaptée en français aux éditions Actes Sud-Papiers (Arles, 1998) par Jean-Marie Besset. Le texte original en anglais de cette pièce est publié aux éditions Faber and Faber, Londres, 1993. Arcadia a obtenu le prix du Syndicat de la critique dramatique de New York.

La pièce se déroule temporellement sur un intervalle d’environ deux siècles dont le début (1809) et la fin (fin des années 1990) sont « entrecroisés » alternativement dans les scènes qui la composent. Il n’existe donc aucune linéarité temporelle dans le cours de la pièce, pas plus d’ailleurs qu’une circularité répétitive, mais plutôt une espèce de « temps chaotique » au cours duquel le temps contemporain fait écho au temps passé, autant que le passé préfigure à sa façon l’époque contemporaine. Mais le passé y est porteur de différences ou ruptures événementielles qui ne se révèlent qu’au moment de la période contemporaine, tandis qu’en cette dernière adviennent des événements dont le germe était plus ou moins repérable au début du siècle précédent. D’où la construction d’Arcadia sur l’idée d’un  temps chaotique, dénué de prévisibilité absolue… Il s’agit d’un temps de la rupture et de l’incertain qui brise en éclats les repères classiques du temps linéaire.

Le texte ci-dessous est repris et adapté de mon article : Temps chaotique et complexité fractale dans Arcadia (1993) de Tom Stoppard, publié dans le recueil intitulé : Temps scientifique, Temps théâtral, éd. C.R.D.P. de Franche-Comté, Besançon, 2001, p. 187-206. Cet ouvrage rassemble les communications du colloque international transdisciplinaire qui fut organisé par le Théâtre universitaire de Franche-Comté et le centre de recherches Jacques-Petit, sur le thème « Temps scientifique, temps théâtral », les 8, 9 et 10 juin 2000.

1. Déterminisme newtonien versus Complexité dynamique dans Arcadia

1.1 – Imprévisibilité et complexité du temps chaotique dans Arcadia

Arcadia, Acte I, scène 1 (Thomasina – Septimus, p. 15-16) ; Acte I, scène 4 (Valentin – Anna, p. 56, 58) ; Acte II, scène 7 (Valentin – Chloé, p. 84 ; Valentin – Anna, p. 89 ; Thomasina – Septimus, p. 92 ; Thomasina – Lady Gray, p. 95 ; Thomasina – Septimus,  p. 99 ; Valentin – Anna – Septimus – Thomasina, p. 105-106). 

L’imprévisibilité et l’incontournable incertitude

La thèse centrale de la théorie scientifique de la complexité repose sur ce postulat : il est impossible de prendre une décision en toute connaissance de cause, car la connaissance humaine doit intégrer l’inévitable « principe d’incertitude », bien connu des physiciens. Ce principe met en jeu l’imprévisibilité des facteurs temporels qui influent sur la trame des phénomènes dynamiques de tous ordres : météorologiques, biologiques, astronomiques, et bien entendu, humains.

Car la vie humaine, comme tout système dynamique, est tout entière tramée d’incer­titude (« de quoi demain sera-t-il fait ? » dit-on souvent). Mais cela ne nous empêche pas de prendre, chaque jour, à nos divers niveaux de respon­sabilité, des décisions qui engagent notre avenir (personnel, familial, politique, etc.), parfois même à l’occasion de circonstances dramatiques. Ces décisions, bonnes ou mau­vaises d’ailleurs, sont prises à partir d’éléments et données d’information dont on dispose à un moment donné, à l’occasion duquel les événements vécus sont appréciés par le décideur.

La question suivante semble par conséquent incontournable : les mauvaises décisions ne seraient-elles pas dues à de mauvaises informations, ou bien à des informations le plus souvent incomplètes…? Si l’on disposait d’une information exhaustive, une telle information ne permettrait-elle pas, dans une situation bien déterminée, de décider en toute connaissance de cause et, par suite, de prévoir avec une quasi-certitude les conséquences de cette décision? Il s’agit là de la question fondamentale posée par les sciences de la complexité, dans toutes ses branches scientifiques.

Le modèle statistique de la complexité climatologique

La complexité des systèmes naturels ou humains fait que cet enchaînement idéal de la transparence intellectuelle de la situation d’une part, de la décision optimale dont les effets ou conséquences sont prévisibles par déduction rationnelle, d’autre part, n’est pas seulement hors de portée de l’intelligence humaine : il est littéralement inconcevable et indescriptible.

Considérons par exemple un problème climatique de plus en plus préoccupant : l’effet de serre. L’activité de l’homme augmente-t­-elle la teneur en gaz carbonique de l’atmosphère et, si c’est le cas, quelles en sont les conséquences prévisibles sur le climat ? Pour s’en tenir à l’examen purement scientifique du problème, la tâche du climatologue consiste à étudier méticuleusement l’évo­lution à long terme d’un système complexe (l’atmosphère terrestre) soumis à de mul­tiples effets matériels extérieurs à lui (rayonnements cos­mique et solaire, échanges avec les océans et le sol, influence de la vie et de l’activité humaine). La difficulté théorique est donc double : il convient en premier lieu de connaître si possible intégralement, exhaustivement, l’état présent du sys­tème climatologique à l’instant t, pour prévoir son évolution future à long terme.

Commençons par la notion, physiquement simple en apparence, de « teneur en gaz carbo­nique de l’atmosphère ». Il s’agit-il d’analyser cette teneur en un point donné du globe, ce qui exige un traitement statistique, qui dégage quelques grandes régularités saison­nières, mais laisse subsister une importante marge d’aléas dus aux intempéries (plus ou moins irrégulières d’une saison à l’autre) en cette région de l’atmosphère terrestre. Mais les physiciens de l’atmosphère parlent de la notion, apparemment moins aléatoire et incertaine, de masse totale de gaz carbonique contenue dans l’atmosphère à un instant donné. Cependant, d’une part nous ne savons pas mesurer celle-ci directement et, d’autre part, rien ne prouve qu’une telle notion soit plus fiable et certaine que la notion précédente.

Pour tenir compte de la complexité du système atmosphérique, la seule définition précise serait celle de la teneur en gaz carbonique en chaque point de l’atmosphère à un instant donné, et pour qu’elle devienne complètement opératoire, on doit la compléter par une très grande masse d’informations physiques, concernant tout aussi bien la direction et la force du vent, la température et la teneur en vapeur d’eau, que les masses océaniques et d’autres paramètres encore. C’est à cette seule condi­tion que l’on pourra déterminer, avec des mesures chiffrées, l’avenir proche du système climatique.

Cette définition du problème climatique de l’effet de serre demande une énorme quantité d’informations complémentaires, qu’il faut mettre en relation au moyen de techniques statistiques complexes. Aussi est-on en droit de se demander s’il n’est pas vain de vouloir résumer par un seul chiffre cette notion climatologique de « teneur en gaz carbonique de l’atmosphère », puisqu’elle se dérobe plus ou moins à l’analyse. Peut-être pourrait-on se contenter de fournir des chiffres caractéristiques, à partir de mesures effectuées tous les cent kilomètres à la sur­face de la Terre et tous les cinq mille mètres en altitude.

La « solution » dépend de l’échelle temporelle à laquelle le climatologue désire obtenir des réponses. En météorologie, ce genre de préci­sions autorise des prévisions à peu près certaines d’un jour à l’autre. Pour prévoir deux jours à l’avance, il faudra disposer de données physiques à une échelle temporelle plus fine. Et plus l’on voudra anticiper, plus il faudra affiner et étendre la trame de ces données, à la fois temporelles et spatiales. Suivant la remarque bien connue du météorologue américain Edward Lorenz (1917-2008), une perturbation météorologique qui ne connaît pas d’entrave à son développement peut doubler en trois jours. Cela signifie que le battement d’ailes 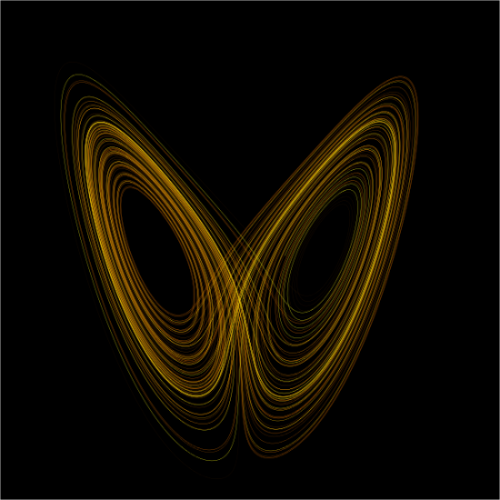d’un papillon en Amazonie en un instant précis peut, si les circonstances lui sont favorables, déclencher une tempête sur les côtes de Bretagne ou de Norvège un an ou dix ans plus tard…

Les physiciens du chaos nomment ce phénomène d’amplification macroscopique la « sensibilité aux conditions initiales » (SCI) : une infime modification des conditions initiales du système (complètement inaperçue) est susceptible d’engendrer, par accumulation ou synergie, des conséquences macrophénoménales incalculables et catastrophiques, modélisables au moyen d'attracteurs étranges. [→ Figure ci-contre : Vue d'un attracteur étrange de Lorenz.] 

En termes équivalents, pour prévoir un an ou dix ans à l’avance le temps qu’il fera en un lieu donné, il faudrait disposer d’un réseau très étendu d’informations qui soit à l’échelle du papillon et qui s’étende sur toute la surface du globe ! Or, si la météorologie est un domaine de prévisions quantitatives à court terme, la climatologie étudie les comportements qualitatifs à long terme. Étant donnée la complexité physique du système, on ne saurait se contenter de données combinées en une moyenne statistique prise sur l’année, même corrigée des fluctuations aléa­toires, pour prévoir la teneur en gaz carbonique de l’atmosphère.

En effet, on n’est pas assuré pour autant de parvenir à plus de certitude : on peut, certes, envisager de grands bilans thermody­namiques, qui permettraient de tirer des conclusions en apparence décisives, mais la dynamique atmosphérique, très instable à l’échelle annuelle, se prêterait sur une période plus longue, de l’ordre du siècle, à des analyses de type statistique qui feraient éventuellement ressortir certaines tendances évolutives. Le temps est le facteur essentiel en thermodynamique, il est pourvoyeur d’événements imprévisibles, qui apportent de la nouveauté à court aussi bien qu’à long terme. De plus, la teneur en gaz carbonique de l’atmosphère, dans cent ou deux cents ans, dépendra de manière cruciale de phénomènes trop fins pour que l’on ait songé aujourd’hui à les inclure dans l’analyse (par exemple, la disparition de certaines espèces animales, et surtout, les nouvelles activités industrielles des sociétés technologiquement avancées).

1.2 – Le déterminisme classique (newtonien) opposé à la science des systèmes dynamiques

Arcadia, Acte I, scène 1 (Thomasina – Septimus, p. 15-16) ; Acte I, scène 4 (Valentin – Anna, p. 56, 58) ; Acte II, scène 7 (Valentin – Chloé, p. 84 ; Valentin – Anna, p. 89 ; Thomasina – Septimus, p. 92 ; Thomasina – Lady Gray, p. 95 ; Thomasina – Septimus,  p. 99 ; Valentin – Anna – Septimus – Thomasina, p. 105-106).

Le déterminisme absolu et la réversibilité du temps dans l’œuvre de Newton

Newton (1642-1727), dans les Principes mathématiques de la philosophie naturelle (1687), a formulé les grands principes du déterminisme classique, auquel s’oppose la théorie des systèmes dynamiques et la thermodynamique elle-même. On peut les résumer ainsi : a) l’explication des phénomènes de la nature suppose qu’existent des causes simples, nécessaires et « suffisantes » ; il n’est pas nécessaire, en somme, de supposer qu’existent des « ruses de la nature » qui viendraient perturber son évolution à long terme; b) c’est pourquoi les causes des effets naturels du même genre sont les mêmes, invariablement. Il n’y a pas de complexité cachée, pour ainsi dire. Le déterminisme classique implique la filiation linéaire de la cause à l’effet, plutôt adéquate dans le champ de la macrophysique, mais peu adaptée à la biologie et surtout aux sciences humaines.

Tout ce qui se produira demain a une cause aujourd’hui, et une connaissance assez précise de la cause permettra de prédire l’effet. La formulation des lois de la nature énoncées par la physique, vise à décrire le changement et les mouvements, caractérisés par une vitesse variant au cours du temps en vertu d’une accélération. L’exemple typique en est la loi formulée par Newton qui lie la force, le mouvement et l’accélération ; cette loi est à la fois déterministe et réversible dans le temps. Connaissant les conditions initiales d’un système sou­mis à cette loi, c’est-à-dire son état en un instant t quel­conque, nous pouvons calculer tous les états suivants aussi bien que tous les états précédents. En outre, le passé et le futur jouent le même rôle, puisque la loi est invariante par rapport à l’inversion des temps (il y a « symétrie temporelle »). La loi de New­ton justifie donc parfaitement le célèbre « démon de Laplace », capable d’observer l’état présent de l’univers et d’en déduire toute l’évolution future, à condition de connaître exactement les conditions initiales du système.

Le développement de la mécanique statistique (mécanique quantique) et la théorie einsteinienne de la relativité ne troubleront guère cette conception du monde, puisque les caractères fondamentaux de la loi causale de Newton, son déterminisme et sa symétrie temporelle, y sont conservés. Le hasard résulte non de l’absence de causes objectives, connues et démontrées, mais de l’addition d’une multitude de petites causes indé­pendantes. On garde ainsi l’espoir que, dans l’avenir, une analyse plus poussée et des méthodes de calcul plus puissantes permettront de révéler le déterminisme caché de phénomènes apparemment aléatoires (suivant l’expression d’Einstein, « Dieu ne joue pas aux dés »). D’ailleurs, le calcul des probabilités et les méthodes statistiques permettent déjà de rendre raison, en apparence, des « lois du hasard » qui affectent la nature.

Mathématiquement, l’outil classique le plus performant pour expliquer le déterminisme, c’est l’équation différentielle. On peut la considérer comme le langage mathématique universel par lequel s’exprime le déterminisme. Si un système est régi par une équation différentielle, son évolution est entièrement ins­crite dans son état présent : la connaissance parfaite de celui-ci permet de reconstituer son passé et de prédire son avenir. Une équation différentielle est une relation instantanée, valable à chaque instant, entre la position d’un mobile, son accélération et sa vitesse. Intégrer (c’est-à-dire résoudre) l’équation différentielle, revient à déduire exactement la trajectoire d’un mobile ainsi que son déplacement sur cette trajectoire, en tout point de celle-ci.

La critique du déterminisme newtonien par Poincaré et le problème des « trois corps » 

Arcadia, Acte I, scène 4, Valentin – Anna, p. 55, 58 ; Acte II, scène 5, Valentin – Bernard – Anna, p. 72, 76 ; Acte II, scène 7, Valentin – Chloé, p. 84, Valentin – Anna, p. 89-90, Thomasina – Septimus, p. 92, 99, Valentin – Anna, p. 105-106.

Donnez-moi les positions et les vitesses actuelles de toutes les particules de l’Univers, disait le mathématicien-astronome Laplace (1749-1827), et je vous calculerai la totalité de son devenir : c’est pour ainsi dire le credo du déterminisme classique absolu. Henri Poincaré (1854-1912) ouvre l’ère scientifique moderne en effectuant la critique du déterminisme classique, à partir de l’analyse du problème de mécanique céleste demeuré célèbre : celui des « trois corps » et de la dynamique chaotique des planètes.

La critique mathématique de Poincaré s’attaque à l’idée même qu’un modèle quantitatif, aussi précis et exact soit-il, comme dans la théorie classique, permette de prévoir intégralement l’avenir avec précision. Ce sont les fondements du credo détermi­niste qui se trouvent ainsi sapés. Il se contenta de montrer que les équations de la dynamique ne sont pas complètement intégrables, et que les séries utilisées pour les résoudre par approximation sont divergentes (elles ne convergent pas vers un résultat numérique fixe et invariable).

Le problème des trois corps permet de bien poser cette nouvelle donne en physique de la complexité. Étant donné trois points matériels représentant des planètes, dont les positions et les vitesses initiales sont connues et qui s’attirent entre eux suivant la loi d’attraction de Newton, il s’agit de calculer leur position à un instant donné du futur – ou du passé, car le processus de calcul est entièrement réversible en analyse classique. On voudrait trouver une formule mathématique, dépendant du temps t et des conditions initiales ; la configuration recherchée devra s’en déduire en donnant une valeur déterminée à la variable t. La formule recherchée sera de la forme : x = f (t), étant entendu que pour trois corps la formule devra permettre de calculer les positions de chacun d’eux à chaque instant du temps.

Poincaré démontre qu’une telle solution n’existe pas, car nous ne sommes pas capables de la calculer. La quantité d’information nécessaire serait énorme pour établir à chaque instant la position et la vitesse en fonction du temps, de ces trois corps simultanément. Car il faudrait reproduire exactement les conditions initiales : si l’on parvenait à reproduire exactement les conditions initiales, on observerait exactement le même mouvement, c’est-à-dire les mêmes configurations aux mêmes instants. Ce qui est en question, c’est la possibilité effective pour l’intelligence humaine indigente, de dégager cette relation et de la traduire, intégralement et fidèlement, en termes effectivement (opératoirement) calculables.

Or, cette perspective est humainement impossible à réaliser. Le traditionnel modèle newtonien de la mécanique céleste recèle, par conséquent, une vérité cachée qui restera toujours en plus ou moins grande partie dissimulée à l’intelligence rationnelle. Dire qu’il n’y a pas de solution complète au problème des trois corps signifie donc qu’il n’y a pas de solution effecti­vement calculable pour toutes les valeurs du temps t, la masse d’informations nécessaires pour le faire étant trop élevée, et la capacité de calcul du cerveau humain étant elle-même nettement insuffisante.

Il s’agit là typiquement d’une question relevant de la théorie de la complexité, au sens contemporain du terme. Le résultat essentiel de Poincaré, c’est que la relation entre le temps et les positions, dans le problème des trois corps, ne peut justement pas s’exprimer à l’aide des fonctions linéaires usuelles. Même si l’on dispose de recettes simples et efficaces pour calculer, par approximation, les valeurs correspondant aux trois corps (les positions de chacun des corps en fonction de la vitesse et du temps), au moyen de calculs en série, en fait les séries infinies utilisées sont divergentes, ce qui signifie qu’elles sont inopérantes pour résoudre le problème ! Les modèles déterministes, soi-disant « exacts », se révèlent donc incapables de prédire une situation complexe.

Ainsi, dans le domaine spécifique de la mécanique céleste (qu’il appelle les « équations de la dynamique »), Henri Poincaré a mis en évidence la complexité globale du mouvement des planètes, en analysant certaines trajectoires particulières et leur voisinage immé­diat. En particulier, il a démontré des situations cosmologiques d’une complexité absolument insoupçonnée, et il a expliqué que les équations de la dynamique pouvaient recouvrir des mouve­ments extrêmement irréguliers, ceux-ci étant d’ailleurs la règle plutôt que l’exception. Sous la régularité apparente, macroscopique, de l’approximation képlérienne (les planètes ont un mouvement absolument régulier et invariable pour Képler), Poincaré a mis en évidence un foisonnement d’accidents microsco­piques, à l’instar d’une particule matérielle qui se révèle, sous le microscope électronique, agitée d’un mouvement brownien permanent, alors qu’on pourrait facilement (et naïvement) l’imaginer au repos.

L’orbite de la Terre, par exemple, est strictement périodi­que selon l’approximation képlérienne, avec une période d’un an, mais ne l’est probablement plus (en prenant en considération une période très longue : plusieurs millions d’années par exemple) si l’on prend en compte les perturbations planétaires. Cependant, Poincaré estime que les solutions périodiques restent précieuses malgré tout, car elles possèdent d’indéniables avantages : notamment, on sait décrire les configurations célestes qui existent autour d’elles, et on sait les calculer, le temps étant supposé « neutre », dans le cas d’une périodicité régulière des planètes, à la manière de Képler.

On ne peut prétendre décrire et prévoir les évolutions des corps célestes comme des évolutions déterministes, qu'à la seule condition nécessaire mais impossible à remplir, de les connaître à tout instant avec une précision absolument infinie. La moindre approximation, même infiniment petite, est fatale, car elle produit la même incertitude qu’une approximation grossière. Il existe un hiatus radical entre le savoir total, attribut divin par excellence, et le savoir humain incertain à jamais, quelle que soit la précision, même quasi illimitée, que celui-ci peut atteindre. C’est toute la problématique anthropologique de la complexité informationnelle qui se voit ainsi résumée et évoquée, dans la pièce de théâtre de Tom Stoppard.

1.3 – L’irréversibilité du temps et l’entropie thermodynamique

Arcadia, Acte I, scène 4, Valentin – Anna, p. 55, 58 ; Acte II, scène 5, Valentin – Bernard – Anna, p. 72, 76 ; Acte II, scène 7, Valentin – Chloé, p. 84, Valentin – Anna, p. 89-90, Thomasina – Septimus, p. 92, 99, Valentin – Anna, p. 105-106.

La loi newtonienne (puis la mécanique quantique) défendait le principe de réversibilité du temps, pour expliquer le déterminisme intégral des lois naturelles. La physique du chaos déterministe, quant à elle, défend le principe de l’irréversibilité temporelle, pourvoyeuse de nouveauté imprévisible. C’est ce que le prix Nobel de chimie, Ilya Prigogine appelle « la flèche du temps ». Cependant, il faut rappeler qu’avant le développement de la physique du chaos et des systèmes dynamiques, la thermodynamique de la fin du dix-neuvième siècle avait déjà apporté l’idée d’une direction du temps et donc celle de son irréversibilité.

Le principe d’entropie est l’élément essentiel introduit par la thermodynamique, la science des processus physiques irréver­sibles, c’est-à-dire orientés dans le temps. Parmi les processus irréversibles, on peut évoquer la décomposition radioactive, la friction mécanique ou la viscosité qui ralentit le mouvement d’un fluide. Ces processus ont une direction privilé­giée dans le temps, en contraste avec les processus réversibles tels que le mouvement d’un pendule idéal, donc abstrait, sans aucune friction mécanique. Une substance radioactive, préparée dans le passé, disparaît dans le futur, et la viscosité ralentit le mouvement du fluide dans le futur. Par contre, dans le mouvement du pendule idéal nous ne pou­vons pas distinguer futur et passé. Si l'on per­mute mathématiquement le futur, symbolisé par + t, avec le passé, symbolisé par − t , nous réobtenons un mouvement pendulaire identique à lui-même, tout aussi plausible que le premier. Tandis que les processus réversibles sont décrits par des équa­tions d’évolution invariantes par rapport à l’inversion des temps, comme l’équation de Newton en dyna­mique classique (c’est valable aussi pour la mécanique quantique), les processus physiques irréversibles impliquent une brisure radicale de la symétrie temporelle.

La nature présente au physicien à la fois des processus irré­versibles et des processus réversibles, mais les pre­miers sont la règle, et les seconds l’exception, expliquent les physiciens de la complexité dynamique. En particulier, les pro­cessus macroscopiques comme les réactions physico-chimiques, les phénomènes thermiques, etc., sont irréversibles. Ainsi, le rayonnement solaire est le résultat de processus nucléaires irréversibles innombrables. Les processus réversibles, en revanche, correspondent toujours à des idéalisations théoriques ; ainsi, pour attribuer au pendule un comportement réversible, il est nécessaire de négliger la friction, et cette démarche n’a de sens qu’à titre d’approximation du processus pendulaire réel.

La distinction entre processus réversibles et irréver­sibles fut introduite en thermodynamique sous la forme du concept d’entropie que Clausius (1822-1888), en 1865, qualifie de « second principe de la thermodynamique ». Clausius formule en ces termes les deux principes de la thermo­dynamique : 1) l’énergie de l’univers est constante ; 2) l’entropie de l’univers croît vers un maximum. Contrairement au principe selon lequel l’énergie se conserverait invariablement, l’entropie thermodynamique permet d’établir une distinction entre les processus idéalement (ou véritablement) réversibles, et les pro­cessus irréversibles, qui produisent de l’entropie, synonyme de « désordre », ou, plus exactement, d’équiprobabilité des configurations évoluant vers des états plus ou moins indéterminés (« désordonnés » au plan statistique), étudiées par le physicien.

Mais, simultanément, une nouvelle compréhension des phénomènes instables, des processus dynamiques dits « de non équilibre » (car irréversibles et évoluant vers des configurations imprévisibles), s’instaurait avec la thermodynamique du dix-neuvième siècle. En effet, la physique du chaos démontre que les processus physico-chimiques peuvent aussi bien évoluer en direction d’une entropie maximale, c’est-à-dire une équiprobabilité statistique synonyme de désordre thermodynamique, qu’en direction de certaines formes d’ordre, imprévisibles et radicalement nouvelles. En fait, la « flèche du temps » est le vecteur ou la source d’ordres insoupçonnables, et en tout cas inimaginables par la physique classique de la réversibilité. Elle instaure la « dissymétrie temporelle » la plus irrévocable qui puisse être pensée en physique, et par conséquent l’imprédictibilité absolue opposée à la raison déterministe.

L’irréversibilité, susceptible d’engendrer des situations de non équilibre naturel, devient un facteur constructif pour la science du chaos et de la complexité spatio-temporelle. Une philosophie possibiliste de la nature a pu ainsi se créer à partir des lois de la thermodynamique de Clausius, en vertu de laquelle la conception de l’émergence de structures possibles est placée au centre de la théorie des phénomènes irréversibles.

La croissance de l’entropie désigne par conséquent la direction du futur, que ce soit au niveau d’un système local ou de l’Univers dans son ensemble : c’est « la flèche du temps », dans le langage d’Ilya Prigogine, flèche du temps qui ne joue traditionnellement aucun rôle dans la formulation des lois fondamentales de la phy­sique newtonienne. Le physicien autricien Ludwig Boltzmann (1844-1906) s’attacha à réconcilier ces deux conceptions en apparence contradictoires des lois de la nature, en mettant au centre des préoccupations de la physique moderne l’idée de processus continu d’évolution, où le devenir des grands ensembles collectifs d’éléments physiques était ainsi mis au centre de notre compréhen­sion statistique de la nature.

→ Suite Partie II

© Jean-Claude Chirollet